| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 8.1) | Exercise 8.1 | Example 6 to 10 (Before Exercise 8.2) |
| Exercise 8.2 | Example 11 to 15 - Miscellaneous Examples | Miscellaneous Exercise on Chapter 8 |
Chapter 8 Application Of Integrals
Welcome to the solutions for Chapter 8: Application of Integrals. Having developed the machinery of definite integration in the previous chapter and understanding its connection to the area under a curve via the Fundamental Theorem of Calculus, we now focus directly on applying this powerful tool to calculate the areas of various planar regions bounded by curves and lines. This chapter provides a concrete geometric interpretation and application for the abstract concept of the definite integral. The ability to calculate areas of complex shapes defined by functions is fundamental in geometry, physics (e.g., calculating work done from a force-displacement graph), engineering (e.g., finding cross-sectional areas), and statistics (e.g., finding probabilities from probability density functions). The core principle revolves around approximating the desired area using infinitesimally thin rectangles and summing their areas, which is precisely what the definite integral accomplishes in the limit.
The solutions demonstrate two primary scenarios for area calculation using definite integrals:
1. Area under Simple Curves: This involves finding the area of a region bounded by a single curve, one of the coordinate axes, and two lines parallel to the other axis.
- If the region is bounded by the curve $y = f(x)$, the x-axis, and the vertical lines $x = a$ and $x = b$, and assuming $f(x) \geq 0$ in the interval $[a, b]$, the area is given by the definite integral: $Area = \int\limits_{a}^{b} y \, dx = \int\limits_{a}^{b} f(x) \, dx$. The solutions emphasize that if the curve $y=f(x)$ lies below the x-axis ($f(x) \leq 0$) in the interval, the definite integral $\int\limits_{a}^{b} f(x) \, dx$ will yield a negative value. Since area must be positive, the required area is the absolute value, $Area = \left| \int\limits_{a}^{b} f(x) \, dx \right| = -\int\limits_{a}^{b} f(x) \, dx$. If the curve crosses the x-axis within the interval, the integral needs to be split at the crossing points.
- Similarly, if the region is bounded by the curve $x = g(y)$, the y-axis, and the horizontal lines $y = c$ and $y = d$, assuming $g(y) \geq 0$ in $[c, d]$, the area is calculated by integrating with respect to $y$: $Area = \int\limits_{c}^{d} x \, dy = \int\limits_{c}^{d} g(y) \, dy$. Analogous considerations apply if the curve is to the left of the y-axis ($g(y) \leq 0$).
A crucial first step highlighted in the solutions for all area problems is accurately sketching the curve(s) involved. This visual representation helps identify the region whose area is required, determine the correct limits of integration ($a, b$ or $c, d$), and decide whether to integrate with respect to $x$ or $y$.
2. Area between Two Curves: This involves finding the area of the region enclosed between two intersecting curves.
- If the region is bounded by two curves $y = f(x)$ and $y = g(x)$, which intersect at $x = a$ and $x = b$, and $f(x) \geq g(x)$ (i.e., $f(x)$ is the "upper" curve) for all $x$ in $[a, b]$, the area is given by: $Area = \int\limits_{a}^{b} [f(x) - g(x)] \, dx = \int\limits_{a}^{b} (\text{Upper Curve} - \text{Lower Curve}) \, dx$. A critical prerequisite shown in the solutions is finding the points of intersection by solving the equation $f(x) = g(x)$ to determine the limits of integration $a$ and $b$.
- Similarly, if the region is bounded by two curves $x = f(y)$ and $x = g(y)$, intersecting at $y = c$ and $y = d$, with $f(y) \geq g(y)$ (i.e., $f(y)$ is the "right" curve) for all $y$ in $[c, d]$, the area is: $Area = \int\limits_{c}^{d} [f(y) - g(y)] \, dy = \int\limits_{c}^{d} (\text{Right Curve} - \text{Left Curve}) \, dy$. Again, finding the intersection points by solving $f(y) = g(y)$ is necessary to find the limits $c$ and $d$.
The problems presented in the solutions typically involve finding areas bounded by common curves like lines, circles (often requiring solving for $y$ in terms of $x$, e.g., $y = \sqrt{r^2 - x^2}$ for a semicircle), parabolas ($y^2=4ax$, $x^2=4ay$), and ellipses. Solutions provide detailed steps for sketching the region, identifying the appropriate upper/lower or right/left functions, finding intersection points algebraically, setting up the correct definite integral (sometimes requiring splitting the region into multiple parts if the upper/lower curve changes), performing the integration using techniques from the previous chapter, and evaluating the definite integral to arrive at the final area.
Example 1 to 5 (Before Exercise 8.1)
Example 1: Find the area enclosed by the circle x2 + y2 = a2 .
Answer:
Given:
Equation of the circle is $x^2 + y^2 = a^2$.
To Find:
Area enclosed by the circle.
Solution:
The given equation of the circle is $x^2 + y^2 = a^2$. This represents a circle centered at the origin $(0,0)$ with radius $a$.
The area enclosed by the circle can be calculated using integration.
From the equation $x^2 + y^2 = a^2$, we can express $y$ in terms of $x$: $y^2 = a^2 - x^2$, so $y = \pm\sqrt{a^2 - x^2}$.
The upper semi-circle is given by $y = \sqrt{a^2 - x^2}$ for $-a \leq x \leq a$.
Due to the symmetry of the circle about both the x and y axes, the total area of the circle is four times the area of the portion lying in the first quadrant.
The area in the first quadrant is bounded by the curve $y = \sqrt{a^2 - x^2}$, the x-axis ($y=0$), the y-axis ($x=0$), and the line $x=a$.
The area in the first quadrant is given by the integral $\int\limits_{0}^{a} \sqrt{a^2 - x^2} \$ dx$.
The total area A of the circle is thus:
$A = 4 \int\limits_{0}^{a} \sqrt{a^2 - x^2} \$ dx$
We use the standard integral formula for $\sqrt{a^2 - x^2}$:
$\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$
Now, we evaluate the definite integral from $0$ to $a$:
$A = 4 \left[\frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}$
Substitute the upper limit $x=a$:
$\left(\frac{a}{2}\sqrt{a^2 - a^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{a}{a}\right)\right) = \left(\frac{a}{2}\sqrt{0} + \frac{a^2}{2}\sin^{-1}(1)\right) = \left(0 + \frac{a^2}{2} \times \frac{\pi}{2}\right) = \frac{\pi a^2}{4}$
Substitute the lower limit $x=0$:
$\left(\frac{0}{2}\sqrt{a^2 - 0^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{0}{a}\right)\right) = \left(0 + \frac{a^2}{2}\sin^{-1}(0)\right) = (0 + 0) = 0$
Now, subtract the value at the lower limit from the value at the upper limit:
$A = 4 \left[ \frac{\pi a^2}{4} - 0 \right]$
$A = 4 \left( \frac{\pi a^2}{4} \right)$
$A = \pi a^2$
Final Answer:
The area enclosed by the circle $x^2 + y^2 = a^2$ is $\pi a^2$ square units.
Example 2: Find the area enclosed by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
Answer:
Given:
The equation of the ellipse is $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$.
To Find:
Area enclosed by the ellipse.
Solution:
The given equation of the ellipse is $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. This ellipse is symmetric about both the x-axis and the y-axis.
The area enclosed by the ellipse can be found by calculating the area of the portion in the first quadrant and multiplying it by 4.
From the equation of the ellipse, we can express $y$ in terms of $x$: $\frac{y^2}{b^2} = 1 - \frac{x^2}{a^2}$
$y^2 = b^2 \left(1 - \frac{x^2}{a^2}\right) = \frac{b^2}{a^2}(a^2 - x^2)$
$y = \pm \frac{b}{a}\sqrt{a^2 - x^2}$
In the first quadrant, $x \ge 0$ and $y \ge 0$, so we take the positive root: $y = \frac{b}{a}\sqrt{a^2 - x^2}$.
The area in the first quadrant is given by the integral of $y$ with respect to $x$ from $x=0$ to $x=a$:
Area in first quadrant $= \int\limits_{0}^{a} y \$ dx = \int\limits_{0}^{a} \frac{b}{a}\sqrt{a^2 - x^2} \$ dx$
$= \frac{b}{a} \int\limits_{0}^{a} \sqrt{a^2 - x^2} \$ dx$
We use the standard integral formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$.
Evaluating the definite integral:
$\int\limits_{0}^{a} \sqrt{a^2 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}$
$= \left(\frac{a}{2}\sqrt{a^2 - a^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{a}{a}\right)\right) - \left(\frac{0}{2}\sqrt{a^2 - 0^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{0}{a}\right)\right)$
$= \left(0 + \frac{a^2}{2}\sin^{-1}(1)\right) - (0 + 0)$
$= \frac{a^2}{2} \times \frac{\pi}{2} = \frac{\pi a^2}{4}$
So, the area in the first quadrant of the ellipse is:
Area in first quadrant $= \frac{b}{a} \times \frac{\pi a^2}{4} = \frac{\pi ab}{4}$
The total area of the ellipse is 4 times the area in the first quadrant:
Total Area $A = 4 \times \frac{\pi ab}{4} = \pi ab$
Final Answer:
The area enclosed by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ is $\pi ab$ square units.
Example 3: Find the area of the region bounded by the curve y = x2 and the line y = 4.
Answer:
Given:
The curve is given by $y = x^2$ and the line is $y = 4$.
To Find:
The area of the region bounded by the curve and the line.
Solution:
The given curve is $y = x^2$, which is a parabola symmetric about the y-axis with its vertex at the origin $(0,0)$.
The given line is $y = 4$, which is a horizontal line.
To find the points of intersection of the parabola and the line, we set the y-values equal:
$x^2 = 4$
Solving for $x$, we get $x = \pm \sqrt{4}$, which means $x = \pm 2$.
The points of intersection are $(-2, 4)$ and $(2, 4)$.
The region bounded by the curve $y = x^2$ and the line $y = 4$ is the area between these two curves from $x = -2$ to $x = 2$.
In the interval $[-2, 2]$, the line $y = 4$ is above the parabola $y = x^2$.
The area of the bounded region can be calculated by integrating the difference between the upper curve and the lower curve with respect to $x$ from the left intersection point to the right intersection point.
Area $A = \int\limits_{-2}^{2} (y_{\text{line}} - y_{\text{parabola}}) \$ dx$
$A = \int\limits_{-2}^{2} (4 - x^2) \$ dx$
Since the region is symmetric about the y-axis, we can calculate the area from $x=0$ to $x=2$ and multiply it by 2.
$A = 2 \int\limits_{0}^{2} (4 - x^2) \$ dx$
Now, we evaluate the integral:
$A = 2 \left[4x - \frac{x^3}{3}\right]_{0}^{2}$
Substitute the upper limit $x=2$:
$4(2) - \frac{2^3}{3} = 8 - \frac{8}{3}$
Substitute the lower limit $x=0$:
$4(0) - \frac{0^3}{3} = 0 - 0 = 0$
Evaluate the definite integral:
$A = 2 \left[ \left(8 - \frac{8}{3}\right) - (0) \right]$
$A = 2 \left(8 - \frac{8}{3}\right)$
$A = 2 \left(\frac{24 - 8}{3}\right)$
$A = 2 \left(\frac{16}{3}\right)$
$A = \frac{32}{3}$
Final Answer:
The area of the region bounded by the curve $y = x^2$ and the line $y = 4$ is $\frac{32}{3}$ square units.
Example 4: Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x, and the circle x2 + y2 = 32.
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. The x-axis ($y = 0$)
2. The line $y = x$
3. The circle $x^2 + y^2 = 32$
To Find:
The area of the specified region in the first quadrant.
Solution:
The bounding curves are the x-axis ($y=0$), the line $y=x$, and the circle $x^2 + y^2 = 32$. We are interested in the region strictly within the first quadrant.
Let's analyze the boundaries in the first quadrant:
- The x-axis corresponds to an angle of $0$ in polar coordinates ($\theta = 0$).
- The line $y=x$ corresponds to an angle of $\pi/4$ in polar coordinates ($\theta = \pi/4$), since $\tan \theta = y/x = 1$, and in the first quadrant, $\theta = \pi/4$.
- The circle $x^2 + y^2 = 32$ can be written in polar coordinates as $r^2 = 32$, so $r = \sqrt{32} = 4\sqrt{2}$ (since $r \ge 0$).
The region in the first quadrant bounded by the x-axis and the line $y=x$ and the circle $x^2+y^2=32$ is a sector of the circle defined by the angles from $\theta=0$ (x-axis) to $\theta=\pi/4$ (line $y=x$), with radius $r = 4\sqrt{2}$.
The area of a region in polar coordinates is given by the formula:
$A = \frac{1}{2} \int\limits_{\theta_1}^{\theta_2} r^2(\theta) \$ d\theta$
In this case, the radius $r$ is constant for the entire sector, $r=4\sqrt{2}$, and the angle $\theta$ ranges from $0$ to $\pi/4$.
$A = \frac{1}{2} \int\limits_{0}^{\pi/4} (4\sqrt{2})^2 \$ d\theta$
$A = \frac{1}{2} \int\limits_{0}^{\pi/4} 32 \$ d\theta$
$A = 16 \int\limits_{0}^{\pi/4} \$ d\theta$
Evaluate the integral:
$A = 16 [\theta]_{0}^{\pi/4}$
$A = 16 \left(\frac{\pi}{4} - 0\right)$
$A = 16 \times \frac{\pi}{4}$
$A = 4\pi$
Alternate Approach (using Cartesian coordinates):
The intersection points in the first quadrant are $(0,0)$, $(4,4)$ (intersection of $y=x$ and circle), and $(4\sqrt{2}, 0)$ (intersection of circle and x-axis).
The region can be split into two parts when integrating with respect to $x$:
Part 1: From $x=0$ to $x=4$, bounded above by $y=x$ and below by $y=0$. Area $A_1 = \int\limits_{0}^{4} x \$ dx$.
Part 2: From $x=4$ to $x=4\sqrt{2}$, bounded above by the circle $y=\sqrt{32-x^2}$ and below by $y=0$. Area $A_2 = \int\limits_{4}^{4\sqrt{2}} \sqrt{32-x^2} \$ dx$.
Total Area $A = A_1 + A_2$
$A_1 = \left[\frac{x^2}{2}\right]_{0}^{4} = \frac{4^2}{2} - \frac{0^2}{2} = \frac{16}{2} - 0 = 8$
$A_2 = \int\limits_{4}^{4\sqrt{2}} \sqrt{32-x^2} \$ dx$. Use the formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$, with $a^2=32$, so $a=4\sqrt{2}$.
$A_2 = \left[\frac{x}{2}\sqrt{32-x^2} + \frac{32}{2}\sin^{-1}\left(\frac{x}{4\sqrt{2}}\right)\right]_{4}^{4\sqrt{2}}$
$A_2 = \left(\frac{4\sqrt{2}}{2}\sqrt{32-(4\sqrt{2})^2} + 16\sin^{-1}\left(\frac{4\sqrt{2}}{4\sqrt{2}}\right)\right) - \left(\frac{4}{2}\sqrt{32-4^2} + 16\sin^{-1}\left(\frac{4}{4\sqrt{2}}\right)\right)$
$A_2 = \left(2\sqrt{2}\sqrt{32-32} + 16\sin^{-1}(1)\right) - \left(2\sqrt{32-16} + 16\sin^{-1}\left(\frac{1}{\sqrt{2}}\right)\right)$
$A_2 = \left(0 + 16 \times \frac{\pi}{2}\right) - \left(2\sqrt{16} + 16 \times \frac{\pi}{4}\right)$
$A_2 = 8\pi - (2 \times 4 + 4\pi)$
$A_2 = 8\pi - (8 + 4\pi)$
$A_2 = 8\pi - 8 - 4\pi = 4\pi - 8$
Total Area $A = A_1 + A_2 = 8 + (4\pi - 8) = 4\pi$
Both methods yield the same result.
Final Answer:
The area of the region in the first quadrant enclosed by the x-axis, the line $y = x$, and the circle $x^2 + y^2 = 32$ is $4\pi$ square units.
Example 5: Find the area bounded by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ and the ordinates x = 0 and x = ae, where, b2 = a2 (1 – e2) and e < 1.
Answer:
Given:
Equation of the ellipse: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$.
Bounding ordinates: $x = 0$ and $x = ae$, where $b^2 = a^2(1-e^2)$ and $e < 1$.
To Find:
The area bounded by the ellipse and the given ordinates.
Solution:
The given equation of the ellipse is $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$.
We need to find the area bounded by this ellipse, the y-axis ($x=0$), and the vertical line $x = ae$. Since $e < 1$, we have $ae < a$. The region lies between $x=0$ and $x=ae$.
From the equation of the ellipse, we can express $y$ in terms of $x$:
$\frac{y^2}{b^2} = 1 - \frac{x^2}{a^2} = \frac{a^2 - x^2}{a^2}$
$y^2 = \frac{b^2}{a^2}(a^2 - x^2)$
$y = \pm \frac{b}{a}\sqrt{a^2 - x^2}$
The ellipse is symmetric about the x-axis. The required area is bounded by the upper half of the ellipse $y = \frac{b}{a}\sqrt{a^2 - x^2}$ and the lower half $y = -\frac{b}{a}\sqrt{a^2 - x^2}$ from $x=0$ to $x=ae$.
Due to symmetry, the total area is twice the area in the first quadrant bounded by the x-axis ($y=0$), $x=0$, $x=ae$, and the curve $y = \frac{b}{a}\sqrt{a^2 - x^2}$.
Area $A = 2 \int\limits_{0}^{ae} y \$ dx = 2 \int\limits_{0}^{ae} \frac{b}{a}\sqrt{a^2 - x^2} \$ dx$
$A = \frac{2b}{a} \int\limits_{0}^{ae} \sqrt{a^2 - x^2} \$ dx$
We use the standard integral formula: $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$.
Now we evaluate the definite integral from $0$ to $ae$:
$\int\limits_{0}^{ae} \sqrt{a^2 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{ae}$
Substitute the upper limit $x=ae$:
$\frac{ae}{2}\sqrt{a^2 - (ae)^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{ae}{a}\right) = \frac{ae}{2}\sqrt{a^2 - a^2e^2} + \frac{a^2}{2}\sin^{-1}(e)$
$= \frac{ae}{2}\sqrt{a^2(1 - e^2)} + \frac{a^2}{2}\sin^{-1}(e) = \frac{ae}{2}a\sqrt{1 - e^2} + \frac{a^2}{2}\sin^{-1}(e)$
Using $b^2 = a^2(1-e^2)$, so $\sqrt{1-e^2} = \frac{b}{a}$ (since $e<1$, $1-e^2 > 0$ and $b>0$):
$= \frac{ae}{2}a\left(\frac{b}{a}\right) + \frac{a^2}{2}\sin^{-1}(e) = \frac{aeb}{2} + \frac{a^2}{2}\sin^{-1}(e)$
Substitute the lower limit $x=0$:
$\frac{0}{2}\sqrt{a^2 - 0^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{0}{a}\right) = 0 + \frac{a^2}{2}\sin^{-1}(0) = 0 + 0 = 0$
So, $\int\limits_{0}^{ae} \sqrt{a^2 - x^2} \$ dx = \left(\frac{aeb}{2} + \frac{a^2}{2}\sin^{-1}(e)\right) - 0 = \frac{aeb}{2} + \frac{a^2}{2}\sin^{-1}(e)$.
Now, substitute this back into the expression for the total area $A$:
$A = \frac{2b}{a} \left(\frac{aeb}{2} + \frac{a^2}{2}\sin^{-1}(e)\right)$
$A = \frac{2b}{a} \times \frac{aeb}{2} + \frac{2b}{a} \times \frac{a^2}{2}\sin^{-1}(e)$
$A = \frac{aeb^2}{a} + \frac{a^2 b}{a}\sin^{-1}(e)$
$A = eb^2 + ab\sin^{-1}(e)$
We can also express this in terms of $a$ and $e$ using $b^2 = a^2(1-e^2)$ and $b = a\sqrt{1-e^2}$:
$A = e(a^2(1-e^2)) + a(a\sqrt{1-e^2})\sin^{-1}(e)$
$A = a^2e(1-e^2) + a^2\sqrt{1-e^2}\sin^{-1}(e)$
Both forms are valid.
Final Answer:
The area bounded by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ and the ordinates $x = 0$ and $x = ae$ is $eb^2 + ab\sin^{-1}(e)$ square units, or $a^2e(1-e^2) + a^2\sqrt{1-e^2}\sin^{-1}(e)$ square units.
Exercise 8.1
Question 1. Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Answer:
Given:
The bounding curves and lines are:
1. Curve: $y^2 = x$
2. Line: $x = 1$
3. Line: $x = 4$
4. The x-axis ($y = 0$)
To Find:
The area of the region bounded by the given curve and lines.
Solution:
The given curve is $y^2 = x$, which is a parabola opening to the right, symmetric about the x-axis. The vertex is at $(0,0)$.
The lines are $x=1$ and $x=4$, which are vertical lines.
The x-axis is the line $y=0$.
We are looking for the area in the region bounded by the parabola, the vertical lines $x=1$ and $x=4$, and the x-axis. Since the parabola is $y^2=x$, for $x \ge 0$, we have $y = \pm\sqrt{x}$. The x-axis ($y=0$) is one of the boundaries. The region bounded by the curve $y^2=x$, the lines $x=1$, $x=4$, and the x-axis is the area above the x-axis (where $y = \sqrt{x}$) between $x=1$ and $x=4$. The region is shown in the first quadrant.
The area of this region is given by the integral of the function $y = \sqrt{x}$ from $x=1$ to $x=4$ with respect to $x$.
Area $A = \int\limits_{1}^{4} y \$ dx$
$A = \int\limits_{1}^{4} \sqrt{x} \$ dx$
$A = \int\limits_{1}^{4} x^{1/2} \$ dx$
Now, we evaluate the integral:
The antiderivative of $x^{1/2}$ is $\frac{x^{1/2 + 1}}{1/2 + 1} = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}$.
$A = \left[\frac{2}{3}x^{3/2}\right]_{1}^{4}$
Substitute the upper limit $x=4$:
$\frac{2}{3}(4)^{3/2} = \frac{2}{3}(\sqrt{4})^3 = \frac{2}{3}(2)^3 = \frac{2}{3}(8) = \frac{16}{3}$
Substitute the lower limit $x=1$:
$\frac{2}{3}(1)^{3/2} = \frac{2}{3}(\sqrt{1})^3 = \frac{2}{3}(1)^3 = \frac{2}{3}(1) = \frac{2}{3}$
Evaluate the definite integral:
$A = \frac{16}{3} - \frac{2}{3}$
$A = \frac{16 - 2}{3}$
$A = \frac{14}{3}$
Final Answer:
The area of the region bounded by the curve $y^2 = x$, the lines $x = 1$, $x = 4$, and the x-axis is $\frac{14}{3}$ square units.
Question 2. Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. Curve: $y^2 = 9x$
2. Line: $x = 2$
3. Line: $x = 4$
4. The x-axis ($y = 0$)
To Find:
The area of the specified region in the first quadrant.
Solution:
The given curve is $y^2 = 9x$, which is a parabola opening to the right with its vertex at the origin $(0,0)$.
The lines are $x=2$ and $x=4$, which are vertical lines.
The x-axis is the line $y=0$.
We are looking for the area in the first quadrant bounded by the parabola $y^2=9x$, the vertical lines $x=2$ and $x=4$, and the x-axis. In the first quadrant, $x \ge 0$ and $y \ge 0$.
From $y^2 = 9x$, for the first quadrant, we take the positive square root: $y = \sqrt{9x} = 3\sqrt{x}$.
The region is bounded above by the curve $y = 3\sqrt{x}$ and below by the x-axis ($y=0$). The boundaries in the x-direction are from $x=2$ to $x=4$.
The area of this region is given by the integral of the function $y = 3\sqrt{x}$ from $x=2$ to $x=4$ with respect to $x$.
Area $A = \int\limits_{2}^{4} y \$ dx$
$A = \int\limits_{2}^{4} 3\sqrt{x} \$ dx$
$A = 3 \int\limits_{2}^{4} x^{1/2} \$ dx$
Now, we evaluate the integral:
The antiderivative of $x^{1/2}$ is $\frac{x^{1/2 + 1}}{1/2 + 1} = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}$.
$A = 3 \left[\frac{2}{3}x^{3/2}\right]_{2}^{4}$
$A = 2 \left[x^{3/2}\right]_{2}^{4}$
Substitute the upper limit $x=4$:
$2 (4)^{3/2} = 2 (\sqrt{4})^3 = 2 (2)^3 = 2(8) = 16$
Substitute the lower limit $x=2$:
$2 (2)^{3/2} = 2 (2\sqrt{2}) = 4\sqrt{2}$
Evaluate the definite integral:
$A = 16 - 4\sqrt{2}$
$A = 4(4 - \sqrt{2})$
Final Answer:
The area of the region bounded by $y^2 = 9x$, $x = 2$, $x = 4$, and the x-axis in the first quadrant is $16 - 4\sqrt{2}$ square units.
Question 3. Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. Curve: $x^2 = 4y$
2. Line: $y = 2$
3. Line: $y = 4$
4. The y-axis ($x = 0$)
To Find:
The area of the specified region in the first quadrant.
Solution:
The given curve is $x^2 = 4y$, which is a parabola opening upwards with its vertex at the origin $(0,0)$.
The lines are $y=2$ and $y=4$, which are horizontal lines.
The y-axis is the line $x=0$.
We are looking for the area in the first quadrant bounded by the parabola $x^2=4y$, the horizontal lines $y=2$ and $y=4$, and the y-axis. In the first quadrant, $x \ge 0$ and $y \ge 0$.
From $x^2 = 4y$, for the first quadrant, we take the positive square root of $x^2$: $x = \sqrt{4y} = 2\sqrt{y}$.
The region is bounded on the left by the y-axis ($x=0$) and on the right by the curve $x = 2\sqrt{y}$. The region extends vertically from $y=2$ to $y=4$.
It is convenient to integrate with respect to $y$. The area of this region is given by the integral of the function $x = 2\sqrt{y}$ from $y=2$ to $y=4$ with respect to $y$.
Area $A = \int\limits_{2}^{4} x \$ dy$
$A = \int\limits_{2}^{4} 2\sqrt{y} \$ dy$
$A = 2 \int\limits_{2}^{4} y^{1/2} \$ dy$
Now, we evaluate the integral:
The antiderivative of $y^{1/2}$ is $\frac{y^{1/2 + 1}}{1/2 + 1} = \frac{y^{3/2}}{3/2} = \frac{2}{3}y^{3/2}$.
$A = 2 \left[\frac{2}{3}y^{3/2}\right]_{2}^{4}$
$A = \frac{4}{3} \left[y^{3/2}\right]_{2}^{4}$
Substitute the upper limit $y=4$:
$(4)^{3/2} = (\sqrt{4})^3 = 2^3 = 8$
Substitute the lower limit $y=2$:
$(2)^{3/2} = (\sqrt{2})^3 = (\sqrt{2})^2 \times \sqrt{2} = 2\sqrt{2}$
Evaluate the definite integral:
$A = \frac{4}{3} (8 - 2\sqrt{2})$
$A = \frac{32}{3} - \frac{8\sqrt{2}}{3}$
$A = \frac{8}{3}(4 - \sqrt{2})$
Final Answer:
The area of the region bounded by $x^2 = 4y$, $y = 2$, $y = 4$, and the y-axis in the first quadrant is $\frac{32}{3} - \frac{8\sqrt{2}}{3}$ square units.
Question 4. Find the area of the region bounded by the ellipse $\frac{x^2}{16} + \frac{y^2}{9} = 1$.
Answer:
Given:
The equation of the ellipse is $\frac{x^2}{16} + \frac{y^2}{9} = 1$.
To Find:
Area enclosed by the ellipse.
Solution:
The given equation of the ellipse is $\frac{x^2}{16} + \frac{y^2}{9} = 1$. This is in the standard form $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, where $a^2 = 16$ and $b^2 = 9$.
Thus, the semi-major axis is $a = \sqrt{16} = 4$ and the semi-minor axis is $b = \sqrt{9} = 3$.
The ellipse is symmetric about both the x-axis and the y-axis.
The area enclosed by the ellipse can be found by calculating the area of the portion in the first quadrant and multiplying it by 4.
From the equation of the ellipse, we can express $y$ in terms of $x$:
$\frac{y^2}{9} = 1 - \frac{x^2}{16}$
$y^2 = 9 \left(1 - \frac{x^2}{16}\right) = \frac{9}{16}(16 - x^2)$
$y = \pm \frac{3}{4}\sqrt{16 - x^2}$
In the first quadrant, $x \ge 0$ and $y \ge 0$, so we take the positive root: $y = \frac{3}{4}\sqrt{16 - x^2}$.
The area in the first quadrant is given by the integral of $y$ with respect to $x$ from $x=0$ to $x=a=4$:
Area in first quadrant $= \int\limits_{0}^{4} y \$ dx = \int\limits_{0}^{4} \frac{3}{4}\sqrt{16 - x^2} \$ dx$
$= \frac{3}{4} \int\limits_{0}^{4} \sqrt{16 - x^2} \$ dx$
We use the standard integral formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$. Here $a=4$.
Evaluating the definite integral:
$\int\limits_{0}^{4} \sqrt{16 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{16 - x^2} + \frac{16}{2}\sin^{-1}\left(\frac{x}{4}\right)\right]_{0}^{4}$
$= \left(\frac{4}{2}\sqrt{16 - 4^2} + 8\sin^{-1}\left(\frac{4}{4}\right)\right) - \left(\frac{0}{2}\sqrt{16 - 0^2} + 8\sin^{-1}\left(\frac{0}{4}\right)\right)$
$= \left(2\sqrt{16 - 16} + 8\sin^{-1}(1)\right) - \left(0 + 8\sin^{-1}(0)\right)$
$= \left(2\sqrt{0} + 8 \times \frac{\pi}{2}\right) - (0 + 0)$
$= (0 + 4\pi) - 0 = 4\pi$
So, the area in the first quadrant of the ellipse is:
Area in first quadrant $= \frac{3}{4} \times 4\pi = 3\pi$
The total area of the ellipse is 4 times the area in the first quadrant:
Total Area $A = 4 \times 3\pi = 12\pi$
Alternatively, using the standard formula for the area of an ellipse with semi-axes $a$ and $b$, Area $= \pi ab$.
Here $a=4$ and $b=3$.
Area $A = \pi \times 4 \times 3 = 12\pi$.
Final Answer:
The area of the region bounded by the ellipse $\frac{x^2}{16} + \frac{y^2}{9} = 1$ is $12\pi$ square units.
Question 5. Find the area of the region bounded by the ellipse $\frac{x^2}{4} + \frac{y^2}{9} = 1$.
Answer:
Given:
The equation of the ellipse is $\frac{x^2}{4} + \frac{y^2}{9} = 1$.
To Find:
Area enclosed by the ellipse.
Solution:
The given equation of the ellipse is $\frac{x^2}{4} + \frac{y^2}{9} = 1$. This is in the standard form $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$.
Comparing the given equation with the standard form, we have $a^2 = 4$ and $b^2 = 9$.
Thus, $a = \sqrt{4} = 2$ and $b = \sqrt{9} = 3$.
The ellipse is centered at the origin and is symmetric about both the x-axis and the y-axis.
The area enclosed by the ellipse can be found by calculating the area of the portion in the first quadrant and multiplying it by 4.
From the equation of the ellipse, we can express $y$ in terms of $x$:
$\frac{y^2}{9} = 1 - \frac{x^2}{4}$
$y^2 = 9 \left(1 - \frac{x^2}{4}\right) = \frac{9}{4}(4 - x^2)$
$y = \pm \frac{3}{2}\sqrt{4 - x^2}$
In the first quadrant, $x \ge 0$ and $y \ge 0$, so we take the positive root: $y = \frac{3}{2}\sqrt{4 - x^2}$.
The area in the first quadrant is bounded by the curve $y = \frac{3}{2}\sqrt{4 - x^2}$, the x-axis ($y=0$), the y-axis ($x=0$), and the line $x=2$ (since the ellipse extends from $x=-2$ to $x=2$).
The area in the first quadrant is given by the integral of $y$ with respect to $x$ from $x=0$ to $x=2$:
Area in first quadrant $= \int\limits_{0}^{2} y \$ dx = \int\limits_{0}^{2} \frac{3}{2}\sqrt{4 - x^2} \$ dx$
$= \frac{3}{2} \int\limits_{0}^{2} \sqrt{2^2 - x^2} \$ dx$
We use the standard integral formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$. Here $a=2$.
Evaluating the definite integral:
$\int\limits_{0}^{2} \sqrt{4 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
$= \left(\frac{2}{2}\sqrt{4 - 2^2} + 2\sin^{-1}\left(\frac{2}{2}\right)\right) - \left(\frac{0}{2}\sqrt{4 - 0^2} + 2\sin^{-1}\left(\frac{0}{2}\right)\right)$
$= \left(1\sqrt{0} + 2\sin^{-1}(1)\right) - (0 + 2\sin^{-1}(0))$
$= (0 + 2 \times \frac{\pi}{2}) - (0 + 0) = \pi$
So, the area in the first quadrant of the ellipse is:
Area in first quadrant $= \frac{3}{2} \times \pi = \frac{3\pi}{2}$
The total area of the ellipse is 4 times the area in the first quadrant:
Total Area $A = 4 \times \frac{3\pi}{2} = 6\pi$
Alternate Approach:
The area of an ellipse with semi-major axis $a$ and semi-minor axis $b$ is given by the formula $\pi ab$.
From the equation $\frac{x^2}{4} + \frac{y^2}{9} = 1$, we have $a^2 = 4$ and $b^2 = 9$. So $a=2$ and $b=3$.
Area $A = \pi \times 2 \times 3 = 6\pi$ square units.
Final Answer:
The area of the region bounded by the ellipse $\frac{x^2}{4} + \frac{y^2}{9} = 1$ is $6\pi$ square units.
Question 6. Find the area of the region in the first quadrant enclosed by x-axis, line x = $\sqrt{3}$ y and the circle x2 + y2 = 4.
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. The x-axis ($y = 0$)
2. The line $x = \sqrt{3}y$
3. The circle $x^2 + y^2 = 4$
To Find:
The area of the specified region in the first quadrant.
Solution:
The bounding curves and lines are the x-axis ($y=0$), the line $x = \sqrt{3}y$, and the circle $x^2 + y^2 = 4$. We are looking for the area in the first quadrant.
The equation of the circle is $x^2 + y^2 = 4$, which is centered at the origin with radius $r = \sqrt{4} = 2$.
The equation of the line is $x = \sqrt{3}y$. We can rewrite this as $y = \frac{1}{\sqrt{3}}x$. This line passes through the origin $(0,0)$.
In the first quadrant, the x-axis corresponds to $\theta = 0$ in polar coordinates.
Let's convert the line $y = \frac{1}{\sqrt{3}}x$ to polar coordinates. Using $x = r\cos\theta$ and $y = r\sin\theta$, we get:
$r\sin\theta = \frac{1}{\sqrt{3}} r\cos\theta$
Since the line passes through the origin, we consider points where $r \ne 0$. Dividing by $r\cos\theta$ (assuming $\cos\theta \ne 0$, which is true in the interior of the first quadrant):
$\tan\theta = \frac{1}{\sqrt{3}}$
In the first quadrant, the angle $\theta$ for which $\tan\theta = \frac{1}{\sqrt{3}}$ is $\theta = \frac{\pi}{6}$.
The region is enclosed by the x-axis ($\theta = 0$), the line $x = \sqrt{3}y$ ($\theta = \pi/6$), and the circle $x^2 + y^2 = 4$ ($r=2$). The region is a sector of the circle in the first quadrant, lying between the angles $\theta = 0$ and $\theta = \pi/6$.
The area of a sector in polar coordinates is given by $A = \frac{1}{2} \int\limits_{\theta_1}^{\theta_2} r^2(\theta) \$ d\theta$.
In this case, the radius $r$ is constant and equal to 2, and the angle $\theta$ ranges from $0$ to $\pi/6$.
$A = \frac{1}{2} \int\limits_{0}^{\pi/6} (2)^2 \$ d\theta$
$A = \frac{1}{2} \int\limits_{0}^{\pi/6} 4 \$ d\theta$
$A = 2 \int\limits_{0}^{\pi/6} \$ d\theta$
Now, we evaluate the integral:
$A = 2 [\theta]_{0}^{\pi/6}$
Substitute the limits:
$A = 2 \left(\frac{\pi}{6} - 0\right)$
$A = 2 \times \frac{\pi}{6}$
$A = \frac{\pi}{3}$
Final Answer:
The area of the region in the first quadrant enclosed by the x-axis, the line $x = \sqrt{3} y$, and the circle $x^2 + y^2 = 4$ is $\frac{\pi}{3}$ square units.
Question 7. Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line $x = \frac{a}{\sqrt{2}}$.
Answer:
Given:
Equation of the circle: $x^2 + y^2 = a^2$.
Equation of the line: $x = \frac{a}{\sqrt{2}}$.
To Find:
The area of the smaller part of the circle cut off by the line.
Solution:
The given equation of the circle is $x^2 + y^2 = a^2$, which represents a circle centered at the origin $(0,0)$ with radius $a$.
The line is $x = \frac{a}{\sqrt{2}}$, which is a vertical line. Since $\frac{1}{\sqrt{2}} < 1$, the line $x = \frac{a}{\sqrt{2}}$ intersects the circle between $x=0$ and $x=a$.
The intersection points of the circle and the line are found by substituting $x = \frac{a}{\sqrt{2}}$ into the circle equation:
$(\frac{a}{\sqrt{2}})^2 + y^2 = a^2$
$\frac{a^2}{2} + y^2 = a^2$
$y^2 = a^2 - \frac{a^2}{2} = \frac{a^2}{2}$
$y = \pm \sqrt{\frac{a^2}{2}} = \pm \frac{a}{\sqrt{2}}$
The intersection points are $(\frac{a}{\sqrt{2}}, \frac{a}{\sqrt{2}})$ and $(\frac{a}{\sqrt{2}}, -\frac{a}{\sqrt{2}})$.
The line $x = \frac{a}{\sqrt{2}}$ cuts the circle into two parts. The smaller part is the region to the right of the line $x = \frac{a}{\sqrt{2}}$, within the circle.
This region is bounded on the left by the line $x = \frac{a}{\sqrt{2}}$ and on the right by the circle. The upper boundary is the curve $y = \sqrt{a^2 - x^2}$ and the lower boundary is $y = -\sqrt{a^2 - x^2}$.
Due to the symmetry of the circle about the x-axis, the area of the smaller part is twice the area in the first quadrant bounded by the line $x = \frac{a}{\sqrt{2}}$, the upper semi-circle $y = \sqrt{a^2 - x^2}$, and the x-axis ($y=0$).
The area in the first quadrant is given by the integral of $y = \sqrt{a^2 - x^2}$ with respect to $x$ from $x = \frac{a}{\sqrt{2}}$ to $x = a$ (the x-coordinate of the rightmost point of the circle).
Area $A = 2 \int\limits_{a/\sqrt{2}}^{a} \sqrt{a^2 - x^2} \$ dx$
We use the standard integral formula: $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$.
Now we evaluate the definite integral from $\frac{a}{\sqrt{2}}$ to $a$:
$A = 2 \left[\frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{a/\sqrt{2}}^{a}$
Substitute the upper limit $x=a$:
$\left(\frac{a}{2}\sqrt{a^2 - a^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{a}{a}\right)\right) = \left(\frac{a}{2}\sqrt{0} + \frac{a^2}{2}\sin^{-1}(1)\right) = 0 + \frac{a^2}{2} \times \frac{\pi}{2} = \frac{\pi a^2}{4}$
Substitute the lower limit $x=\frac{a}{\sqrt{2}}$:
$\left(\frac{a/\sqrt{2}}{2}\sqrt{a^2 - (\frac{a}{\sqrt{2}})^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{a/\sqrt{2}}{a}\right)\right) = \left(\frac{a}{2\sqrt{2}}\sqrt{a^2 - \frac{a^2}{2}} + \frac{a^2}{2}\sin^{-1}\left(\frac{1}{\sqrt{2}}\right)\right)$
$= \left(\frac{a}{2\sqrt{2}}\sqrt{\frac{a^2}{2}} + \frac{a^2}{2}\sin^{-1}\left(\frac{1}{\sqrt{2}}\right)\right) = \left(\frac{a}{2\sqrt{2}} \times \frac{a}{\sqrt{2}} + \frac{a^2}{2} \times \frac{\pi}{4}\right)$
$= \left(\frac{a^2}{4} + \frac{\pi a^2}{8}\right)$
Evaluate the definite integral:
$A = 2 \left[ \left(\frac{\pi a^2}{4}\right) - \left(\frac{a^2}{4} + \frac{\pi a^2}{8}\right) \right]$
$A = 2 \left[ \frac{\pi a^2}{4} - \frac{a^2}{4} - \frac{\pi a^2}{8} \right]$
$A = 2 \left[ \frac{2\pi a^2 - 2a^2 - \pi a^2}{8} \right]$
$A = 2 \left[ \frac{\pi a^2 - 2a^2}{8} \right]$
$A = \frac{\pi a^2 - 2a^2}{4}$
$A = \frac{a^2}{4}(\pi - 2)$
Final Answer:
The area of the smaller part of the circle $x^2 + y^2 = a^2$ cut off by the line $x = \frac{a}{\sqrt{2}}$ is $\frac{a^2}{4}(\pi - 2)$ square units.
Question 8. The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Answer:
Given:
The region is bounded by the curve $x = y^2$ and the line $x = 4$.
The line $x = a$ divides the area of this region into two equal parts.
To Find:
The value of $a$.
Solution:
The given curve is $x = y^2$, which is a parabola opening to the right, symmetric about the x-axis.
The line is $x = 4$, which is a vertical line.
The region bounded by the parabola $x=y^2$ and the line $x=4$ extends from $x=0$ (the vertex of the parabola) to $x=4$. The upper boundary of this region is $y = \sqrt{x}$ and the lower boundary is $y = -\sqrt{x}$ (for $x \ge 0$).
The width of the region at a given value of $x$ is $\sqrt{x} - (-\sqrt{x}) = 2\sqrt{x}$.
The total area of the region bounded by $x=y^2$ and $x=4$ is given by the integral of this width from $x=0$ to $x=4$.
Total Area $A_{total} = \int\limits_{0}^{4} 2\sqrt{x} \$ dx = 2 \int\limits_{0}^{4} x^{1/2} \$ dx$
$A_{total} = 2 \left[\frac{x^{3/2}}{3/2}\right]_{0}^{4} = 2 \left[\frac{2}{3}x^{3/2}\right]_{0}^{4} = \frac{4}{3} \left[x^{3/2}\right]_{0}^{4}$
$A_{total} = \frac{4}{3} (4^{3/2} - 0^{3/2}) = \frac{4}{3} ((\sqrt{4})^3 - 0) = \frac{4}{3} (2^3) = \frac{4}{3} (8) = \frac{32}{3}$
The line $x=a$ divides this total area into two equal parts. These two parts are the area bounded by $x=y^2$ and $x=a$ (for $0 \le x \le a$) and the area bounded by $x=a$ and $x=4$ (for $a \le x \le 4$).
Let's consider the area of the part of the region for $0 \le x \le a$. This area is given by:
Area ($0 \le x \le a$) $= \int\limits_{0}^{a} 2\sqrt{x} \$ dx$
Area ($0 \le x \le a$) $= 2 \int\limits_{0}^{a} x^{1/2} \$ dx = 2 \left[\frac{2}{3}x^{3/2}\right]_{0}^{a} = \frac{4}{3} \left[x^{3/2}\right]_{0}^{a}$
Area ($0 \le x \le a$) $= \frac{4}{3} (a^{3/2} - 0^{3/2}) = \frac{4}{3} a^{3/2}$
According to the problem, the line $x=a$ divides the total area into two equal parts. This means the area from $0$ to $a$ is equal to the area from $a$ to $4$.
Area ($0 \le x \le a$) = Area ($a \le x \le 4$)
Also, Area ($0 \le x \le a$) + Area ($a \le x \le 4$) = Total Area $A_{total}$.
So, Area ($0 \le x \le a$) $= \frac{1}{2} A_{total}$.
$\frac{4}{3} a^{3/2} = \frac{1}{2} \times \frac{32}{3}$
$\frac{4}{3} a^{3/2} = \frac{16}{3}$
Multiply both sides by $\frac{3}{4}$:
$a^{3/2} = \frac{16}{3} \times \frac{3}{4}$
$a^{3/2} = 4$
To solve for $a$, raise both sides to the power of $\frac{2}{3}$:
$(a^{3/2})^{2/3} = 4^{2/3}$
$a = (2^2)^{2/3} = 2^{2 \times \frac{2}{3}} = 2^{4/3}$
The value of $a$ is $2^{4/3}$. This value is between $2^1=2$ and $2^2=4$, so $0 < a < 4$, which is consistent with the line $x=a$ dividing the region between $x=0$ and $x=4$.
Final Answer:
The value of $a$ is $2^{4/3}$.
Question 9. Find the area of the region bounded by the parabola y = x2 and y = |x| .
Answer:
Given:
The bounding curves are $y = x^2$ and $y = |x|$.
To Find:
The area of the region bounded by the given curves.
Solution:
The given curves are $y = x^2$ and $y = |x|$.
The curve $y = |x|$ can be defined as:
$y = \begin{cases} x & , & x \geq 0 \\ -x & , & x < 0 \end{cases}$
The curve $y = x^2$ is a parabola opening upwards, symmetric about the y-axis.
The curve $y = |x|$ is a V-shaped graph, also symmetric about the y-axis.
To find the points of intersection, we set the equations equal to each other.
For $x \ge 0$, we have $x^2 = x$.
$x^2 - x = 0$
$x(x - 1) = 0$
This gives $x = 0$ or $x = 1$. The corresponding y-values are $y = 0^2 = 0$ and $y = 1^2 = 1$. The intersection points for $x \ge 0$ are $(0, 0)$ and $(1, 1)$.
For $x < 0$, we have $x^2 = -x$.
$x^2 + x = 0$
$x(x + 1) = 0$
This gives $x = 0$ or $x = -1$. Since we are considering $x < 0$, we take $x = -1$. The corresponding y-value is $y = (-1)^2 = 1$. The intersection point for $x < 0$ is $(-1, 1)$. The point $(0,0)$ is also an intersection point and occurs at the boundary between $x \ge 0$ and $x < 0$.
The intersection points are $(-1, 1)$, $(0, 0)$, and $(1, 1)$. The region bounded by the two curves lies between $x = -1$ and $x = 1$.
In the interval $(-1, 1)$, the graph of $y = |x|$ is above the graph of $y = x^2$. For instance, at $x=0.5$, $|0.5|=0.5$ and $(0.5)^2=0.25$, and $0.5 > 0.25$.
The area of the bounded region is given by the integral of the difference between the upper curve and the lower curve from $x = -1$ to $x = 1$.
Area $A = \int\limits_{-1}^{1} (|x| - x^2) \$ dx$
Since the region is symmetric about the y-axis (both functions are even), we can calculate the area in the first quadrant (from $x=0$ to $x=1$) and multiply it by 2.
For $x \ge 0$, $|x| = x$.
Area $A = 2 \int\limits_{0}^{1} (x - x^2) \$ dx$
Now, we evaluate the integral:
$A = 2 \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1}$
Substitute the upper limit $x=1$:
$\left(\frac{1^2}{2} - \frac{1^3}{3}\right) = \left(\frac{1}{2} - \frac{1}{3}\right) = \frac{3 - 2}{6} = \frac{1}{6}$
Substitute the lower limit $x=0$:
$\left(\frac{0^2}{2} - \frac{0^3}{3}\right) = (0 - 0) = 0$
Evaluate the definite integral:
$A = 2 \left[ \frac{1}{6} - 0 \right] = 2 \times \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$
Final Answer:
The area of the region bounded by the parabola $y = x^2$ and $y = |x|$ is $\frac{1}{3}$ square units.
Question 10. Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
Answer:
Given:
The bounding curves are the parabola $x^2 = 4y$ and the line $x = 4y - 2$.
To Find:
The area of the region bounded by the given curve and line.
Solution:
The given curve is $x^2 = 4y$, which can be written as $y = \frac{x^2}{4}$. This is a parabola opening upwards.
The given line is $x = 4y - 2$. We can express $y$ in terms of $x$: $4y = x + 2$, so $y = \frac{x + 2}{4}$.
To find the points of intersection, we set the y-values equal:
$\frac{x^2}{4} = \frac{x + 2}{4}$
Multiply both sides by 4:
$x^2 = x + 2$
Rearrange into a quadratic equation:
$x^2 - x - 2 = 0$
Factor the quadratic equation:
$(x - 2)(x + 1) = 0$
The solutions for $x$ are $x = 2$ and $x = -1$.
Now, find the corresponding y-values using $y = \frac{x^2}{4}$:
If $x = 2$, $y = \frac{2^2}{4} = \frac{4}{4} = 1$. The intersection point is $(2, 1)$.
If $x = -1$, $y = \frac{(-1)^2}{4} = \frac{1}{4}$. The intersection point is $(-1, 1/4)$.
The region bounded by the parabola and the line is between $x = -1$ and $x = 2$.
To determine which curve is above the other in this interval, we can test a value of $x$ between -1 and 2, say $x=0$.
For the parabola, $y = \frac{0^2}{4} = 0$.
For the line, $y = \frac{0 + 2}{4} = \frac{2}{4} = \frac{1}{2}$.
Since $\frac{1}{2} > 0$, the line $y = \frac{x+2}{4}$ is above the parabola $y = \frac{x^2}{4}$ in the interval $[-1, 2]$.
The area of the bounded region is given by the integral of the difference between the upper curve and the lower curve from $x = -1$ to $x = 2$.
Area $A = \int\limits_{-1}^{2} \left(\text{y}_{\text{line}} - \text{y}_{\text{parabola}}\right) \$ dx
$A = \int\limits_{-1}^{2} \left(\frac{x + 2}{4} - \frac{x^2}{4}\right) \$ dx$
$A = \frac{1}{4} \int\limits_{-1}^{2} (x + 2 - x^2) \$ dx$
Now, we evaluate the integral:
$A = \frac{1}{4} \left[\frac{x^2}{2} + 2x - \frac{x^3}{3}\right]_{-1}^{2}$
Substitute the upper limit $x=2$:
$\left(\frac{2^2}{2} + 2(2) - \frac{2^3}{3}\right) = \left(\frac{4}{2} + 4 - \frac{8}{3}\right) = \left(2 + 4 - \frac{8}{3}\right) = \left(6 - \frac{8}{3}\right) = \left(\frac{18 - 8}{3}\right) = \frac{10}{3}$
Substitute the lower limit $x=-1$:
$\left(\frac{(-1)^2}{2} + 2(-1) - \frac{(-1)^3}{3}\right) = \left(\frac{1}{2} - 2 - \left(-\frac{1}{3}\right)\right) = \left(\frac{1}{2} - 2 + \frac{1}{3}\right)$
$= \left(\frac{3}{6} - \frac{12}{6} + \frac{2}{6}\right) = \frac{3 - 12 + 2}{6} = \frac{-7}{6}$
Evaluate the definite integral:
$A = \frac{1}{4} \left[ \left(\frac{10}{3}\right) - \left(-\frac{7}{6}\right) \right]$
$A = \frac{1}{4} \left[ \frac{10}{3} + \frac{7}{6} \right]$
$A = \frac{1}{4} \left[ \frac{20}{6} + \frac{7}{6} \right]$
$A = \frac{1}{4} \left[ \frac{27}{6} \right]$
$A = \frac{1}{4} \times \frac{\cancel{27}^{9}}{\cancel{6}_{2}}$
$A = \frac{9}{8}$
Final Answer:
The area bounded by the curve $x^2 = 4y$ and the line $x = 4y - 2$ is $\frac{9}{8}$ square units.
Question 11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
Answer:
Given:
The bounding curve is $y^2 = 4x$.
The bounding line is $x = 3$.
To Find:
The area of the region bounded by the given curve and line.
Solution:
The given curve is $y^2 = 4x$. This is a parabola opening to the right, symmetric about the x-axis, with its vertex at the origin $(0,0)$.
The given line is $x = 3$, which is a vertical line.
The region bounded by the parabola $y^2 = 4x$ and the line $x=3$ is the area enclosed between these two curves from $x=0$ to $x=3$.
For $x \ge 0$, $y^2 = 4x$ gives $y = \pm\sqrt{4x} = \pm 2\sqrt{x}$.
The upper half of the parabola is given by $y = 2\sqrt{x}$ and the lower half by $y = -2\sqrt{x}$.
Due to the symmetry of the parabola about the x-axis, the total area of the bounded region is twice the area in the first quadrant bounded by the curve $y = 2\sqrt{x}$, the x-axis ($y=0$), and the line $x=3$.
The area in the first quadrant is given by the integral of $y = 2\sqrt{x}$ with respect to $x$ from $x=0$ to $x=3$.
Area in first quadrant $= \int\limits_{0}^{3} 2\sqrt{x} \$ dx$
$= 2 \int\limits_{0}^{3} x^{1/2} \$ dx$
Now, we evaluate the integral:
The antiderivative of $x^{1/2}$ is $\frac{x^{1/2 + 1}}{1/2 + 1} = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}$.
Area in first quadrant $= 2 \left[\frac{2}{3}x^{3/2}\right]_{0}^{3}$
$= \frac{4}{3} \left[x^{3/2}\right]_{0}^{3}$
Substitute the upper limit $x=3$:
$(3)^{3/2} = 3\sqrt{3}$
Substitute the lower limit $x=0$:
$(0)^{3/2} = 0$
Evaluate the definite integral:
Area in first quadrant $= \frac{4}{3} (3\sqrt{3} - 0) = \frac{4}{3} \times 3\sqrt{3} = 4\sqrt{3}$
The total area of the bounded region is twice the area in the first quadrant:
Total Area $A = 2 \times (4\sqrt{3}) = 8\sqrt{3}$
Final Answer:
The area of the region bounded by the curve $y^2 = 4x$ and the line $x = 3$ is $8\sqrt{3}$ square units.
Choose the correct answer in the following Exercises 12 and 13.
Question 12. Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
(A) π
(B) $\frac{π}{2}$
(C) $\frac{π}{3}$
(D) $\frac{π}{4}$
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. Circle: $x^2 + y^2 = 4$
2. Line: $x = 0$ (y-axis)
3. Line: $x = 2$
To Find:
The area of the specified region in the first quadrant.
Solution:
The equation of the circle is $x^2 + y^2 = 4$, which is centered at the origin $(0,0)$ with radius $r = \sqrt{4} = 2$.
The lines are $x = 0$ (the y-axis) and $x = 2$.
We are interested in the area in the first quadrant bounded by these curves.
In the first quadrant, $x \ge 0$ and $y \ge 0$. The circle $x^2 + y^2 = 4$ in the first quadrant is described by $y = \sqrt{4 - x^2}$ for $0 \le x \le 2$.
The given boundaries $x=0$ and $x=2$ exactly cover the range of x-values for the quarter circle in the first quadrant.
The area of the region is given by the integral of $y = \sqrt{4 - x^2}$ with respect to $x$ from $x=0$ to $x=2$.
Area $A = \int\limits_{0}^{2} \sqrt{4 - x^2} \$ dx$
This is a standard integral of the form $\int \sqrt{a^2 - x^2} \$ dx$, where $a=2$.
The formula is $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$.
Evaluating the definite integral from $0$ to $2$:
$A = \left[\frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
$A = \left[\frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
Substitute the upper limit $x=2$:
$\left(\frac{2}{2}\sqrt{4 - 2^2} + 2\sin^{-1}\left(\frac{2}{2}\right)\right) = \left(1\sqrt{4 - 4} + 2\sin^{-1}(1)\right) = (1\sqrt{0} + 2 \times \frac{\pi}{2}) = (0 + \pi) = \pi$
Substitute the lower limit $x=0$:
$\left(\frac{0}{2}\sqrt{4 - 0^2} + 2\sin^{-1}\left(\frac{0}{2}\right)\right) = \left(0\sqrt{4} + 2\sin^{-1}(0)\right) = (0 + 2 \times 0) = 0$
Evaluate the definite integral:
$A = \pi - 0 = \pi$
Alternate Method:
The region described is the quarter of the circle $x^2+y^2=4$ that lies in the first quadrant. The circle has radius $r=2$.
The area of a full circle is $\pi r^2$. The area of the quarter circle in the first quadrant is $\frac{1}{4}$ of the total area.
Area $= \frac{1}{4} (\pi r^2) = \frac{1}{4} \pi (2)^2 = \frac{1}{4} \pi (4) = \pi$
Final Answer:
The area of the region is $\pi$ square units.
Comparing with the given options, the correct answer is (A) $\pi$.
Question 13. Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is
(A) 2
(B) $\frac{9}{4}$
(C) $\frac{9}{3}$
(D) $\frac{9}{2}$
Answer:
Given:
The bounding curves and line are:
1. Curve: $y^2 = 4x$
2. Line: y-axis ($x = 0$)
3. Line: $y = 3$
To Find:
The area of the region bounded by the given curve and lines.
Solution:
The given curve is $y^2 = 4x$, which is a parabola opening to the right with its vertex at the origin $(0,0)$.
The line is $y = 3$, which is a horizontal line.
The y-axis is the line $x = 0$.
The region is bounded on the left by the y-axis ($x=0$), on the right by the parabola $y^2 = 4x$, below by the x-axis (since the parabola starts at the origin), and above by the line $y=3$.
From the equation of the parabola $y^2 = 4x$, we can express $x$ in terms of $y$: $x = \frac{y^2}{4}$.
The region extends vertically from $y=0$ (the vertex on the y-axis) to $y=3$.
The area of this region is conveniently calculated by integrating with respect to $y$. The area is given by the integral of the function $x = \frac{y^2}{4}$ from $y=0$ to $y=3$ with respect to $y$.
Area $A = \int\limits_{0}^{3} x \$ dy$
$A = \int\limits_{0}^{3} \frac{y^2}{4} \$ dy$
$A = \frac{1}{4} \int\limits_{0}^{3} y^2 \$ dy$
Now, we evaluate the integral:
The antiderivative of $y^2$ is $\frac{y^3}{3}$.
$A = \frac{1}{4} \left[\frac{y^3}{3}\right]_{0}^{3}$
$A = \frac{1}{12} \left[y^3\right]_{0}^{3}$
Substitute the upper limit $y=3$:
$3^3 = 27$
Substitute the lower limit $y=0$:
$0^3 = 0$
Evaluate the definite integral:
$A = \frac{1}{12} (27 - 0)$
$A = \frac{27}{12}$
Simplify the fraction:
$A = \frac{\cancel{27}^{9}}{\cancel{12}_{4}}$
$A = \frac{9}{4}$
Final Answer:
The area of the region bounded by the curve $y^2 = 4x$, the y-axis, and the line $y = 3$ is $\frac{9}{4}$ square units.
Comparing with the given options, the correct answer is (B) $\frac{9}{4}$.
Example 6 to 10 (Before Exercise 8.2)
Example 6: Find the area of the region bounded by the two parabolas y = x2 and y2 = x.
Answer:
Given:
The bounding curves are the parabola $y = x^2$ and the parabola $y^2 = x$.
To Find:
The area of the region bounded by the given curves.
Solution:
The given curves are $y = x^2$ and $y^2 = x$.
The curve $y = x^2$ is a parabola opening upwards, symmetric about the y-axis.
The curve $y^2 = x$ is a parabola opening to the right, symmetric about the x-axis.
To find the points of intersection, we substitute $y = x^2$ from the first equation into the second equation:
$(x^2)^2 = x$
$x^4 = x$
$x^4 - x = 0$
$x(x^3 - 1) = 0$
$x(x - 1)(x^2 + x + 1) = 0$
The real solutions are obtained from $x = 0$ and $x - 1 = 0$. The term $x^2 + x + 1$ has no real roots (since its discriminant is $1^2 - 4(1)(1) = -3 < 0$).
So, the real intersection points occur when $x = 0$ and $x = 1$.
When $x = 0$, from $y = x^2$, we get $y = 0^2 = 0$. Intersection point is $(0, 0)$.
When $x = 1$, from $y = x^2$, we get $y = 1^2 = 1$. Intersection point is $(1, 1)$.
The region bounded by the two parabolas lies between $x = 0$ and $x = 1$.
For $x$ values in the interval $(0, 1)$, we need to determine which curve is above the other.
Consider a value like $x = 0.5$ (which is between 0 and 1):
For $y = x^2$, $y = (0.5)^2 = 0.25$.
For $y^2 = x$, in the region bounded by the two curves and originating from $(0,0)$, we are considering the part of $y^2=x$ in the first quadrant, which is $y = \sqrt{x}$. So, $y = \sqrt{0.5} \approx 0.707$.
Since $0.707 > 0.25$, the curve $y = \sqrt{x}$ (from $y^2=x$) is above the curve $y = x^2$ in the interval $(0, 1)$.
The area of the bounded region is given by the integral of the difference between the upper curve ($y = \sqrt{x}$) and the lower curve ($y = x^2$) with respect to $x$ from the left intersection point ($x=0$) to the right intersection point ($x=1$).
Area $A = \int\limits_{0}^{1} (\sqrt{x} - x^2) \$ dx$
$A = \int\limits_{0}^{1} (x^{1/2} - x^2) \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^{1/2+1}}{1/2+1} - \frac{x^{2+1}}{2+1}\right]_{0}^{1}$
$A = \left[\frac{x^{3/2}}{3/2} - \frac{x^3}{3}\right]_{0}^{1}$
$A = \left[\frac{2}{3}x^{3/2} - \frac{1}{3}x^3\right]_{0}^{1}$
Substitute the upper limit $x=1$:
$\left(\frac{2}{3}(1)^{3/2} - \frac{1}{3}(1)^3\right) = \left(\frac{2}{3}(1) - \frac{1}{3}(1)\right) = \frac{2}{3} - \frac{1}{3} = \frac{1}{3}$
Substitute the lower limit $x=0$:
$\left(\frac{2}{3}(0)^{3/2} - \frac{1}{3}(0)^3\right) = (0 - 0) = 0$
Evaluate the definite integral:
$A = \frac{1}{3} - 0 = \frac{1}{3}$
Final Answer:
The area of the region bounded by the two parabolas $y = x^2$ and $y^2 = x$ is $\frac{1}{3}$ square units.
Example 7: Find the area lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Answer:
Given:
The region is above the x-axis and is bounded by the curves:
1. Circle: $x^2 + y^2 = 8x$
2. Parabola: $y^2 = 4x$
To Find:
The area of the specified region above the x-axis.
Solution:
The equation of the parabola is $y^2 = 4x$. For the region above the x-axis ($y \ge 0$), we have $y = \sqrt{4x} = 2\sqrt{x}$. This parabola has its vertex at the origin $(0,0)$ and opens to the right.
The equation of the circle is $x^2 + y^2 = 8x$. We can rewrite this by completing the square:
$x^2 - 8x + y^2 = 0$
$(x^2 - 8x + 16) + y^2 = 16$
$(x - 4)^2 + y^2 = 4^2$
This is a circle with center $(4, 0)$ and radius $4$. It passes through the origin $(0,0)$ since $(0-4)^2 + 0^2 = 16 + 0 = 16$.
To find the points of intersection of the parabola and the circle, substitute $y^2 = 4x$ into the circle equation:
$x^2 + 4x = 8x$
$x^2 - 4x = 0$
$x(x - 4) = 0$
This gives $x = 0$ or $x = 4$.
Using $y^2 = 4x$ to find the corresponding y-values:
If $x = 0$, $y^2 = 4(0) = 0 \implies y = 0$. Intersection point is $(0, 0)$.
If $x = 4$, $y^2 = 4(4) = 16 \implies y = \pm 4$. Intersection points are $(4, 4)$ and $(4, -4)$.
We are looking for the area above the x-axis, so the relevant intersection points are $(0,0)$ and $(4,4)$. The region is bounded by the upper half of the parabola $y=2\sqrt{x}$ and the upper half of the circle $(x-4)^2 + y^2 = 16$. The upper half of the circle is given by $y = \sqrt{16 - (x-4)^2}$.
The region starts at $x=0$ and extends to $x=4$. In the interval $(0, 4)$, the upper boundary is the circle and the lower boundary is the parabola.
Consider a test point $x=1$ in the interval $(0,4)$.
For the parabola, $y = 2\sqrt{1} = 2$.
For the circle, $y = \sqrt{16 - (1-4)^2} = \sqrt{16 - (-3)^2} = \sqrt{16 - 9} = \sqrt{7}$.
Since $\sqrt{7} \approx 2.65 > 2$, the circle is above the parabola in the interval $(0, 4)$.
The area of the bounded region above the x-axis is the integral of the difference between the upper curve and the lower curve from $x = 0$ to $x = 4$.
Area $A = \int\limits_{0}^{4} \left(\sqrt{16 - (x-4)^2} - 2\sqrt{x}\right) \$ dx$
$A = \int\limits_{0}^{4} \sqrt{16 - (x-4)^2} \$ dx - \int\limits_{0}^{4} 2\sqrt{x} \$ dx$
Let's evaluate the second integral first:
$\int\limits_{0}^{4} 2\sqrt{x} \$ dx = 2 \int\limits_{0}^{4} x^{1/2} \$ dx = 2 \left[\frac{x^{3/2}}{3/2}\right]_{0}^{4} = 2 \left[\frac{2}{3}x^{3/2}\right]_{0}^{4} = \frac{4}{3} \left[x^{3/2}\right]_{0}^{4}$
$= \frac{4}{3} (4^{3/2} - 0^{3/2}) = \frac{4}{3} ((\sqrt{4})^3 - 0) = \frac{4}{3} (2^3) = \frac{4}{3} (8) = \frac{32}{3}$
Now, let's evaluate the first integral: $\int\limits_{0}^{4} \sqrt{16 - (x-4)^2} \$ dx$.
Let $u = x - 4$. Then $du = dx$. When $x=0$, $u = 0 - 4 = -4$. When $x=4$, $u = 4 - 4 = 0$.
The integral becomes $\int\limits_{-4}^{0} \sqrt{16 - u^2} \$ du$.
This is the integral of $\sqrt{a^2 - u^2}$ with $a=4$. The formula is $\int \sqrt{a^2 - u^2} \$ du = \frac{u}{2}\sqrt{a^2 - u^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{u}{a}\right)$.
$\int\limits_{-4}^{0} \sqrt{16 - u^2} \$ du = \left[\frac{u}{2}\sqrt{16 - u^2} + \frac{16}{2}\sin^{-1}\left(\frac{u}{4}\right)\right]_{-4}^{0}$
$= \left[\frac{u}{2}\sqrt{16 - u^2} + 8\sin^{-1}\left(\frac{u}{4}\right)\right]_{-4}^{0}$
Substitute the upper limit $u=0$:
$\left(\frac{0}{2}\sqrt{16 - 0^2} + 8\sin^{-1}\left(\frac{0}{4}\right)\right) = (0 + 8\sin^{-1}(0)) = 0 + 8(0) = 0$
Substitute the lower limit $u=-4$:
$\left(\frac{-4}{2}\sqrt{16 - (-4)^2} + 8\sin^{-1}\left(\frac{-4}{4}\right)\right) = \left(-2\sqrt{16 - 16} + 8\sin^{-1}(-1)\right) = (-2\sqrt{0} + 8 \times (-\frac{\pi}{2})) = 0 - 4\pi = -4\pi$
Evaluate the definite integral:
$\int\limits_{-4}^{0} \sqrt{16 - u^2} \$ du = 0 - (-4\pi) = 4\pi$
This integral represents the area under the upper semi-circle $(x-4)^2 + y^2 = 16$ from $x=0$ to $x=4$. This is indeed the area of a quarter circle with radius 4.
Now, combine the results of the two integrals to find the total area:
$A = 4\pi - \frac{32}{3}$
Final Answer:
The area lying above x-axis and included between the circle $x^2 + y^2 = 8x$ and the parabola $y^2 = 4x$ is $4\pi - \frac{32}{3}$ square units.
Example 8: In Fig 8.17, AOBA is the part of the ellipse 9x2 + y2 = 36 in the first quadrant such that OA = 2 and OB = 6. Find the area between the arc AB and the chord AB.
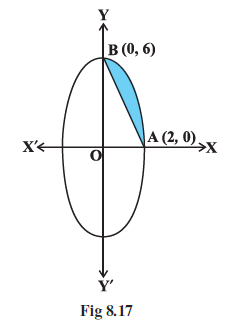
Answer:
Given:
The equation of the ellipse is $9x^2 + y^2 = 36$.
The points A and B are in the first quadrant such that OA = 2 and OB = 6.
The region is bounded by the arc AB and the chord AB.
To Find:
The area between the arc AB and the chord AB.
Solution:
The given equation of the ellipse is $9x^2 + y^2 = 36$.
Divide by 36 to put the equation in standard form:
$\frac{9x^2}{36} + \frac{y^2}{36} = \frac{36}{36}$
$\frac{x^2}{4} + \frac{y^2}{36} = 1$
This is the equation of an ellipse with $a^2 = 4$ and $b^2 = 36$. Thus, $a = \sqrt{4} = 2$ and $b = \sqrt{36} = 6$.
Since $b > a$, the major axis is along the y-axis. The vertices are $(\pm a, 0)$ and $(0, \pm b)$.
In the first quadrant, the ellipse intersects the x-axis at $(a, 0) = (2, 0)$ and the y-axis at $(0, b) = (0, 6)$.
Given that OA = 2 and OB = 6, point A is $(2, 0)$ (on the x-axis) and point B is $(0, 6)$ (on the y-axis). These points are indeed the vertices of the ellipse on the positive x and y axes, respectively.
The area between the arc AB and the chord AB is the area of the region bounded by the arc AB and the line segment (chord) AB.
This area can be calculated as the area of the region under the arc AB (bounded by the ellipse, the x-axis, and the y-axis in the first quadrant) minus the area of the triangle OAB.
The area of the region under the arc AB in the first quadrant is the area of the quarter ellipse. From the ellipse equation, for $y \ge 0$, $y^2 = 36(1 - \frac{x^2}{4}) = 9(4 - x^2)$, so $y = 3\sqrt{4 - x^2}$.
The area under the arc AB is given by the integral of $y = 3\sqrt{4 - x^2}$ from $x=0$ to $x=2$.
Area (under arc AB) $= \int\limits_{0}^{2} 3\sqrt{4 - x^2} \$ dx = 3 \int\limits_{0}^{2} \sqrt{2^2 - x^2} \$ dx$
Using the formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$ with $a=2$:
$= 3 \left[\frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
$= 3 \left[\frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
Evaluating at the limits:
$= 3 \left[ \left(\frac{2}{2}\sqrt{4 - 2^2} + 2\sin^{-1}\left(\frac{2}{2}\right)\right) - \left(\frac{0}{2}\sqrt{4 - 0^2} + 2\sin^{-1}\left(\frac{0}{2}\right)\right) \right]$
$= 3 \left[ (1\sqrt{0} + 2\sin^{-1}(1)) - (0 + 2\sin^{-1}(0)) \right]$
$= 3 \left[ (0 + 2 \times \frac{\pi}{2}) - (0 + 0) \right]$
$= 3 \left[ \pi - 0 \right] = 3\pi$
Alternatively, the area of the quarter ellipse in the first quadrant with semi-axes $a=2$ and $b=6$ is $\frac{1}{4}\pi ab = \frac{1}{4}\pi (2)(6) = 3\pi$.
The area of the triangle OAB with vertices O(0,0), A(2,0), and B(0,6) is given by:
Area (Triangle OAB) $= \frac{1}{2} \times \text{base} \times \text{height}$
The base OA lies on the x-axis and has length 2. The height OB lies on the y-axis and has length 6.
Area (Triangle OAB) $= \frac{1}{2} \times 2 \times 6 = 6$
The area between the arc AB and the chord AB is the difference between the area under the arc and the area of the triangle.
Area (between arc and chord) = Area (under arc AB) - Area (Triangle OAB)
Area $= 3\pi - 6$
Final Answer:
The area between the arc AB and the chord AB is $3\pi - 6$ square units.
Example 9: Using integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1).
Answer:
Given:
The vertices of the triangle are A(1, 0), B(2, 2), and C(3, 1).
To Find:
The area of the region bounded by the triangle using integration.
Solution:
To find the area of the triangle using integration, we first find the equations of the lines joining the vertices.
Equation of line AB:
Points A(1, 0) and B(2, 2).
The slope $m_{AB} = \frac{2 - 0}{2 - 1} = \frac{2}{1} = 2$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with A(1, 0):
$y - 0 = 2(x - 1)$
$y = 2x - 2$
Equation of line BC:
Points B(2, 2) and C(3, 1).
The slope $m_{BC} = \frac{1 - 2}{3 - 2} = \frac{-1}{1} = -1$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with B(2, 2):
$y - 2 = -1(x - 2)$
$y - 2 = -x + 2$
$y = -x + 4$
Equation of line AC:
Points A(1, 0) and C(3, 1).
The slope $m_{AC} = \frac{1 - 0}{3 - 1} = \frac{1}{2}$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with A(1, 0):
$y - 0 = \frac{1}{2}(x - 1)$
$y = \frac{1}{2}x - \frac{1}{2}$
The area of the triangle can be calculated as the area of the region under AB (from $x=1$ to $x=2$) plus the area of the region under BC (from $x=2$ to $x=3$), minus the area of the region under AC (from $x=1$ to $x=3$). This is because AC forms the lower boundary of the triangle across the entire x-range [1, 3], while AB and BC form the upper boundaries over sub-intervals [1, 2] and [2, 3] respectively.
Area of Triangle = Area under AB from $x=1$ to $x=2$ + Area under BC from $x=2$ to $x=3$ - Area under AC from $x=1$ to $x=3$
Area $= \int\limits_{1}^{2} (2x - 2) \$ dx + \int\limits_{2}^{3} (-x + 4) \$ dx - \int\limits_{1}^{3} \left(\frac{1}{2}x - \frac{1}{2}\right) \$ dx$
Evaluate the first integral:
$\int\limits_{1}^{2} (2x - 2) \$ dx = \left[x^2 - 2x\right]_{1}^{2}$
$= (2^2 - 2(2)) - (1^2 - 2(1))$
$= (4 - 4) - (1 - 2) = 0 - (-1) = 1$
Evaluate the second integral:
$\int\limits_{2}^{3} (-x + 4) \$ dx = \left[-\frac{x^2}{2} + 4x\right]_{2}^{3}$
$= \left(-\frac{3^2}{2} + 4(3)\right) - \left(-\frac{2^2}{2} + 4(2)\right)$
$= \left(-\frac{9}{2} + 12\right) - \left(-\frac{4}{2} + 8\right)$
$= \left(-\frac{9}{2} + \frac{24}{2}\right) - (-2 + 8)$
$= \frac{15}{2} - 6 = \frac{15}{2} - \frac{12}{2} = \frac{3}{2}$
Evaluate the third integral:
$\int\limits_{1}^{3} \left(\frac{1}{2}x - \frac{1}{2}\right) \$ dx = \left[\frac{1}{2}\frac{x^2}{2} - \frac{1}{2}x\right]_{1}^{3} = \left[\frac{x^2}{4} - \frac{x}{2}\right]_{1}^{3}$
$= \left(\frac{3^2}{4} - \frac{3}{2}\right) - \left(\frac{1^2}{4} - \frac{1}{2}\right)$
$= \left(\frac{9}{4} - \frac{6}{4}\right) - \left(\frac{1}{4} - \frac{2}{4}\right)$
$= \frac{3}{4} - \left(-\frac{1}{4}\right) = \frac{3}{4} + \frac{1}{4} = \frac{4}{4} = 1$
Total Area $= 1 + \frac{3}{2} - 1 = \frac{3}{2}$
Alternate Method (Integrating difference between curves):
The area can also be computed as the sum of integrals of the difference between the upper and lower curves over the relevant x-intervals.
From $x=1$ to $x=2$, the upper boundary is AB ($y = 2x-2$) and the lower boundary is AC ($y = \frac{1}{2}x - \frac{1}{2}$).
From $x=2$ to $x=3$, the upper boundary is BC ($y = -x+4$) and the lower boundary is AC ($y = \frac{1}{2}x - \frac{1}{2}$).
Area $= \int\limits_{1}^{2} \left((2x - 2) - \left(\frac{1}{2}x - \frac{1}{2}\right)\right) \$ dx + \int\limits_{2}^{3} \left((-x + 4) - \left(\frac{1}{2}x - \frac{1}{2}\right)\right) \$ dx$
Area $= \int\limits_{1}^{2} \left(\frac{3}{2}x - \frac{3}{2}\right) \$ dx + \int\limits_{2}^{3} \left(-\frac{3}{2}x + \frac{9}{2}\right) \$ dx$
Evaluate the first integral:
$\int\limits_{1}^{2} \left(\frac{3}{2}x - \frac{3}{2}\right) \$ dx = \left[\frac{3}{2}\frac{x^2}{2} - \frac{3}{2}x\right]_{1}^{2} = \left[\frac{3}{4}x^2 - \frac{3}{2}x\right]_{1}^{2}$
$= \left(\frac{3}{4}(2)^2 - \frac{3}{2}(2)\right) - \left(\frac{3}{4}(1)^2 - \frac{3}{2}(1)\right)$
$= (3 - 3) - \left(\frac{3}{4} - \frac{6}{4}\right) = 0 - \left(-\frac{3}{4}\right) = \frac{3}{4}$
Evaluate the second integral:
$\int\limits_{2}^{3} \left(-\frac{3}{2}x + \frac{9}{2}\right) \$ dx = \left[-\frac{3}{2}\frac{x^2}{2} + \frac{9}{2}x\right]_{2}^{3} = \left[-\frac{3}{4}x^2 + \frac{9}{2}x\right]_{2}^{3}$
$= \left(-\frac{3}{4}(3)^2 + \frac{9}{2}(3)\right) - \left(-\frac{3}{4}(2)^2 + \frac{9}{2}(2)\right)$
$= \left(-\frac{27}{4} + \frac{27}{2}\right) - (-3 + 9)$
$= \left(-\frac{27}{4} + \frac{54}{4}\right) - 6 = \frac{27}{4} - \frac{24}{4} = \frac{3}{4}$
Total Area $= \frac{3}{4} + \frac{3}{4} = \frac{6}{4} = \frac{3}{2}$
Final Answer:
The area of the region bounded by the triangle with vertices (1, 0), (2, 2), and (3, 1) is $\frac{3}{2}$ square units.
Example 10: Find the area of the region enclosed between the two circles: x2 + y2 = 4 and (x – 2)2 + y2 = 4.
Answer:
Given:
The equations of the two circles are:
Circle 1: $x^2 + y^2 = 4$
Circle 2: $(x - 2)^2 + y^2 = 4$
To Find:
The area of the region enclosed between the two circles.
Solution:
Circle 1 has its center at $C_1 = (0,0)$ and radius $r_1 = \sqrt{4} = 2$.
Circle 2 has its center at $C_2 = (2,0)$ and radius $r_2 = \sqrt{4} = 2$.
To find the points of intersection of the two circles, we set the expressions for $y^2$ equal:
From Circle 1: $y^2 = 4 - x^2$
From Circle 2: $y^2 = 4 - (x - 2)^2$
So, $4 - x^2 = 4 - (x - 2)^2$
$-x^2 = -(x^2 - 4x + 4)$
$-x^2 = -x^2 + 4x - 4$
$0 = 4x - 4$
$4x = 4$
$x = 1$
Now substitute $x = 1$ into the equation of Circle 1 (or Circle 2) to find the y-coordinates of the intersection points:
$1^2 + y^2 = 4$
$1 + y^2 = 4$
$y^2 = 3$
$y = \pm \sqrt{3}$
The intersection points are $(1, \sqrt{3})$ and $(1, -\sqrt{3})$.
The region enclosed between the two circles is the lens-shaped area between these two intersection points. This region is symmetric about the x-axis.
We can calculate the area of the upper half of the region (above the x-axis) and multiply it by 2.
The upper half of the bounded region is composed of two parts:
1. The area under the arc of Circle 2 ($y = \sqrt{4 - (x-2)^2}$) from $x = 0$ to $x = 1$.
2. The area under the arc of Circle 1 ($y = \sqrt{4 - x^2}$) from $x = 1$ to $x = 2$.
Area of upper half $= \int\limits_{0}^{1} \sqrt{4 - (x - 2)^2} \$ dx + \int\limits_{1}^{2} \sqrt{4 - x^2} \$ dx$
We use the standard integral formula: $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$.
For the first integral, let $u = x - 2$, so $du = dx$. When $x = 0$, $u = -2$. When $x = 1$, $u = -1$. The integral is $\int\limits_{-2}^{-1} \sqrt{4 - u^2} \$ du$. Here $a = 2$.
$\int\limits_{-2}^{-1} \sqrt{4 - u^2} \$ du = \left[\frac{u}{2}\sqrt{4 - u^2} + \frac{4}{2}\sin^{-1}\left(\frac{u}{2}\right)\right]_{-2}^{-1}$
$= \left[\frac{u}{2}\sqrt{4 - u^2} + 2\sin^{-1}\left(\frac{u}{2}\right)\right]_{-2}^{-1}$
$= \left(\frac{-1}{2}\sqrt{4 - (-1)^2} + 2\sin^{-1}\left(\frac{-1}{2}\right)\right) - \left(\frac{-2}{2}\sqrt{4 - (-2)^2} + 2\sin^{-1}\left(\frac{-2}{2}\right)\right)$
$= \left(-\frac{1}{2}\sqrt{3} + 2 \left(-\frac{\pi}{6}\right)\right) - \left(-1\sqrt{4 - 4} + 2\left(-\frac{\pi}{2}\right)\right)$
$= \left(-\frac{\sqrt{3}}{2} - \frac{\pi}{3}\right) - (0 - \pi) = -\frac{\sqrt{3}}{2} - \frac{\pi}{3} + \pi = \frac{2\pi}{3} - \frac{\sqrt{3}}{2}$
For the second integral, $\int\limits_{1}^{2} \sqrt{4 - x^2} \$ dx$. Here $a = 2$.
$\int\limits_{1}^{2} \sqrt{4 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right)\right]_{1}^{2}$
$= \left[\frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right)\right]_{1}^{2}$
$= \left(\frac{2}{2}\sqrt{4 - 2^2} + 2\sin^{-1}\left(\frac{2}{2}\right)\right) - \left(\frac{1}{2}\sqrt{4 - 1^2} + 2\sin^{-1}\left(\frac{1}{2}\right)\right)$
$= \left(1\sqrt{0} + 2\sin^{-1}(1)\right) - \left(\frac{1}{2}\sqrt{3} + 2\sin^{-1}\left(\frac{1}{2}\right)\right)$
$= \left(0 + 2 \times \frac{\pi}{2}\right) - \left(\frac{\sqrt{3}}{2} + 2 \times \frac{\pi}{6}\right)$
$= \pi - \left(\frac{\sqrt{3}}{2} + \frac{\pi}{3}\right) = \pi - \frac{\sqrt{3}}{2} - \frac{\pi}{3} = \frac{2\pi}{3} - \frac{\sqrt{3}}{2}$
The area of the upper half is the sum of these two integrals:
Area of upper half $= \left(\frac{2\pi}{3} - \frac{\sqrt{3}}{2}\right) + \left(\frac{2\pi}{3} - \frac{\sqrt{3}}{2}\right) = \frac{4\pi}{3} - \sqrt{3}$
The total area of the region enclosed between the two circles is twice the area of the upper half:
Total Area $A = 2 \times \left(\frac{4\pi}{3} - \sqrt{3}\right) = \frac{8\pi}{3} - 2\sqrt{3}$
Final Answer:
The area of the region enclosed between the two circles $x^2 + y^2 = 4$ and $(x – 2)^2 + y^2 = 4$ is $\frac{8\pi}{3} - 2\sqrt{3}$ square units.
Exercise 8.2
Question 1. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Answer:
Given:
The curves are the circle $4x^2 + 4y^2 = 9$ and the parabola $x^2 = 4y$.
To Find:
The area of the region that is inside the circle and also inside the parabola.
Solution:
The equation of the circle is $4x^2 + 4y^2 = 9$. Dividing by 4, we get $x^2 + y^2 = \frac{9}{4}$. This is a circle centered at the origin $(0,0)$ with radius $r = \sqrt{\frac{9}{4}} = \frac{3}{2}$.
The equation of the parabola is $x^2 = 4y$, which can be written as $y = \frac{x^2}{4}$. This is a parabola opening upwards with its vertex at the origin $(0,0)$.
To find the points of intersection of the circle and the parabola, substitute $x^2 = 4y$ into the equation of the circle:
$4y + y^2 = \frac{9}{4}$
Multiply the entire equation by 4 to clear the fraction:
$16y + 4y^2 = 9$
Rearrange into a quadratic equation in $y$:
$4y^2 + 16y - 9 = 0$
Solve for $y$ using the quadratic formula $y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:
$y = \frac{-16 \pm \sqrt{16^2 - 4(4)(-9)}}{2(4)}$
$y = \frac{-16 \pm \sqrt{256 + 144}}{8}$
$y = \frac{-16 \pm \sqrt{400}}{8}$
$y = \frac{-16 \pm 20}{8}$
Two possible values for $y$ are:
$y_1 = \frac{-16 + 20}{8} = \frac{4}{8} = \frac{1}{2}$
$y_2 = \frac{-16 - 20}{8} = \frac{-36}{8} = -\frac{9}{2}$
Since the parabola $x^2 = 4y$ opens upwards, $y$ must be non-negative for real values of $x$. Thus, the intersection points occur only at $y = \frac{1}{2}$.
Substitute $y = \frac{1}{2}$ back into $x^2 = 4y$ to find the x-coordinates:
$x^2 = 4\left(\frac{1}{2}\right) = 2$
$x = \pm \sqrt{2}$
The intersection points are $(\sqrt{2}, \frac{1}{2})$ and $(-\sqrt{2}, \frac{1}{2})$.
The region whose area is required is the area inside the circle ($x^2 + y^2 \le 9/4$) and interior to the parabola ($x^2 \le 4y$, or $y \ge x^2/4$). This is the region bounded below by the parabola $y = x^2/4$ and bounded above by the circle $y = \sqrt{9/4 - x^2}$ (the upper semi-circle), between the x-values of the intersection points, i.e., from $x = -\sqrt{2}$ to $x = \sqrt{2}$.
Due to the symmetry of the region about the y-axis, we can calculate the area from $x=0$ to $x=\sqrt{2}$ and multiply it by 2.
The area of the region is given by the integral:
$A = \int\limits_{-\sqrt{2}}^{\sqrt{2}} \left(\sqrt{\frac{9}{4} - x^2} - \frac{x^2}{4}\right) \$ dx$
Using symmetry:
$A = 2 \int\limits_{0}^{\sqrt{2}} \left(\sqrt{\frac{9}{4} - x^2} - \frac{x^2}{4}\right) \$ dx$
$A = 2 \left( \int\limits_{0}^{\sqrt{2}} \sqrt{\left(\frac{3}{2}\right)^2 - x^2} \$ dx - \int\limits_{0}^{\sqrt{2}} \frac{x^2}{4} \$ dx \right)$
Evaluate the first integral using the formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$, with $a = \frac{3}{2}$:
$\int\limits_{0}^{\sqrt{2}} \sqrt{\frac{9}{4} - x^2} \$ dx = \left[\frac{x}{2}\sqrt{\frac{9}{4} - x^2} + \frac{9/4}{2}\sin^{-1}\left(\frac{x}{3/2}\right)\right]_{0}^{\sqrt{2}}$
$= \left[\frac{x}{2}\sqrt{\frac{9}{4} - x^2} + \frac{9}{8}\sin^{-1}\left(\frac{2x}{3}\right)\right]_{0}^{\sqrt{2}}$
Substitute the upper limit $x=\sqrt{2}$:
$\frac{\sqrt{2}}{2}\sqrt{\frac{9}{4} - (\sqrt{2})^2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) = \frac{\sqrt{2}}{2}\sqrt{\frac{9}{4} - 2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
$= \frac{\sqrt{2}}{2}\sqrt{\frac{9 - 8}{4}} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) = \frac{\sqrt{2}}{2}\sqrt{\frac{1}{4}} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
$= \frac{\sqrt{2}}{2} \times \frac{1}{2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) = \frac{\sqrt{2}}{4} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
Substitute the lower limit $x=0$:
$\frac{0}{2}\sqrt{\frac{9}{4} - 0^2} + \frac{9}{8}\sin^{-1}\left(\frac{2(0)}{3}\right) = 0 + \frac{9}{8}\sin^{-1}(0) = 0$
Value of the first integral: $\frac{\sqrt{2}}{4} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
Evaluate the second integral:
$\int\limits_{0}^{\sqrt{2}} \frac{x^2}{4} \$ dx = \frac{1}{4} \int\limits_{0}^{\sqrt{2}} x^2 \$ dx = \frac{1}{4} \left[\frac{x^3}{3}\right]_{0}^{\sqrt{2}}$
$= \frac{1}{12} \left[(\sqrt{2})^3 - 0^3\right] = \frac{1}{12} (2\sqrt{2}) = \frac{\sqrt{2}}{6}$
Value of the second integral: $\frac{\sqrt{2}}{6}$
Now substitute the values back into the expression for $A$:
$A = 2 \left( \left(\frac{\sqrt{2}}{4} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)\right) - \frac{\sqrt{2}}{6} \right)$
$A = 2 \left( \frac{\sqrt{2}}{4} - \frac{\sqrt{2}}{6} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) \right)$
Combine the terms with $\sqrt{2}$:
$\frac{\sqrt{2}}{4} - \frac{\sqrt{2}}{6} = \frac{3\sqrt{2}}{12} - \frac{2\sqrt{2}}{12} = \frac{\sqrt{2}}{12}$
So,
$A = 2 \left( \frac{\sqrt{2}}{12} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) \right)$
Distribute the 2:
$A = \frac{2\sqrt{2}}{12} + \frac{18}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
$A = \frac{\sqrt{2}}{6} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
Final Answer:
The area of the region of the circle $4x^2 + 4y^2 = 9$ which is interior to the parabola $x^2 = 4y$ is $\frac{\sqrt{2}}{6} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$ square units.
Question 2. Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y2 = 1.
Answer:
Given:
The bounding curves are the two circles:
Circle 1: $(x - 1)^2 + y^2 = 1$
Circle 2: $x^2 + y^2 = 1$
To Find:
The area of the region bounded by the two circles.
Solution:
The equation of the first circle is $(x - 1)^2 + y^2 = 1$. This is a circle centered at $(1, 0)$ with radius $r_1 = 1$.
The equation of the second circle is $x^2 + y^2 = 1$. This is a circle centered at $(0, 0)$ with radius $r_2 = 1$.
To find the points of intersection of the two circles, we set the expressions for $y^2$ equal:
From Circle 1: $y^2 = 1 - (x - 1)^2$
From Circle 2: $y^2 = 1 - x^2$
So, $1 - (x - 1)^2 = 1 - x^2$
$1 - (x^2 - 2x + 1) = 1 - x^2$
$1 - x^2 + 2x - 1 = 1 - x^2$
$2x - x^2 = 1 - x^2$
$2x = 1$
$x = \frac{1}{2}$
Substitute $x = \frac{1}{2}$ into the equation of Circle 2 ($x^2 + y^2 = 1$) to find the y-coordinates of the intersection points:
$(\frac{1}{2})^2 + y^2 = 1$
$\frac{1}{4} + y^2 = 1$
$y^2 = 1 - \frac{1}{4} = \frac{3}{4}$
$y = \pm \sqrt{\frac{3}{4}} = \pm \frac{\sqrt{3}}{2}$
The intersection points are $(\frac{1}{2}, \frac{\sqrt{3}}{2})$ and $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$.
The region bounded by the two circles is the lens-shaped area between the intersection points. This region is symmetric about the x-axis. We can calculate the area by integrating with respect to y.
We need to express x in terms of y for both circles:
From Circle 1: $(x - 1)^2 = 1 - y^2 \implies x - 1 = \pm\sqrt{1 - y^2} \implies x = 1 \pm\sqrt{1 - y^2}$. The left arc is $x = 1 - \sqrt{1 - y^2}$.
From Circle 2: $x^2 = 1 - y^2 \implies x = \pm\sqrt{1 - y^2}$. The right arc is $x = \sqrt{1 - y^2}$.
The region extends vertically from $y = -\frac{\sqrt{3}}{2}$ to $y = \frac{\sqrt{3}}{2}$. For a given value of y in this range, the right boundary of the region is given by the arc of Circle 2 ($x = \sqrt{1 - y^2}$) and the left boundary is given by the arc of Circle 1 ($x = 1 - \sqrt{1 - y^2}$).
The area of the bounded region is given by the integral:
Area $A = \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} (x_{\text{right}} - x_{\text{left}}) \$ dy$
$A = \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} (\sqrt{1 - y^2} - (1 - \sqrt{1 - y^2})) \$ dy$
$A = \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} (\sqrt{1 - y^2} - 1 + \sqrt{1 - y^2}) \$ dy$
$A = \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} (2\sqrt{1 - y^2} - 1) \$ dy$
$A = 2 \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} \sqrt{1 - y^2} \$ dy - \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} 1 \$ dy$
We use the standard integral formula $\int \sqrt{a^2 - y^2} \$ dy = \frac{y}{2}\sqrt{a^2 - y^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{y}{a}\right)$. Here $a=1$.
Evaluate the first part of the integral: $\int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} \sqrt{1 - y^2} \$ dy = \left[\frac{y}{2}\sqrt{1 - y^2} + \frac{1}{2}\sin^{-1}(y)\right]_{-\sqrt{3}/2}^{\sqrt{3}/2}$
Substitute the upper limit $y=\frac{\sqrt{3}}{2}$:
$\frac{\sqrt{3}/2}{2}\sqrt{1 - (\frac{\sqrt{3}}{2})^2} + \frac{1}{2}\sin^{-1}\left(\frac{\sqrt{3}}{2}\right) = \frac{\sqrt{3}}{4}\sqrt{1 - \frac{3}{4}} + \frac{1}{2}\frac{\pi}{3} = \frac{\sqrt{3}}{4}\sqrt{\frac{1}{4}} + \frac{\pi}{6} = \frac{\sqrt{3}}{4}\frac{1}{2} + \frac{\pi}{6} = \frac{\sqrt{3}}{8} + \frac{\pi}{6}$
Substitute the lower limit $y=-\frac{\sqrt{3}}{2}$:
$\frac{-\sqrt{3}/2}{2}\sqrt{1 - (-\frac{\sqrt{3}}{2})^2} + \frac{1}{2}\sin^{-1}\left(-\frac{\sqrt{3}}{2}\right) = -\frac{\sqrt{3}}{4}\sqrt{1 - \frac{3}{4}} + \frac{1}{2}\left(-\frac{\pi}{3}\right) = -\frac{\sqrt{3}}{4}\frac{1}{2} - \frac{\pi}{6} = -\frac{\sqrt{3}}{8} - \frac{\pi}{6}$
Value of the first integral: $\left(\frac{\sqrt{3}}{8} + \frac{\pi}{6}\right) - \left(-\frac{\sqrt{3}}{8} - \frac{\pi}{6}\right) = \frac{\sqrt{3}}{8} + \frac{\pi}{6} + \frac{\sqrt{3}}{8} + \frac{\pi}{6} = \frac{2\sqrt{3}}{8} + \frac{2\pi}{6} = \frac{\sqrt{3}}{4} + \frac{\pi}{3}$.
So, $2 \int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} \sqrt{1 - y^2} \$ dy = 2 \left(\frac{\sqrt{3}}{4} + \frac{\pi}{3}\right) = \frac{\sqrt{3}}{2} + \frac{2\pi}{3}$.
Evaluate the second part of the integral: $\int\limits_{-\sqrt{3}/2}^{\sqrt{3}/2} 1 \$ dy = [y]_{-\sqrt{3}/2}^{\sqrt{3}/2} = \frac{\sqrt{3}}{2} - \left(-\frac{\sqrt{3}}{2}\right) = \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} = \sqrt{3}$.
Total Area $A = \left(\frac{\sqrt{3}}{2} + \frac{2\pi}{3}\right) - \sqrt{3} = \frac{2\pi}{3} + \frac{\sqrt{3}}{2} - \sqrt{3} = \frac{2\pi}{3} - \frac{\sqrt{3}}{2}$.
Alternate Method (Sum of Segments):
The area is the sum of two circular segments, one from each circle, cut off by the common chord (the line $x = 1/2$).
For Circle 2 ($x^2 + y^2 = 1$), centered at $(0,0)$ with radius $r=1$, the chord is $x=1/2$. The distance from the center to the chord is $d = 1/2$. The angle $\theta$ subtended by the chord at the center is $2 \times \cos^{-1}(d/r) = 2 \times \cos^{-1}(1/2) = 2 \times \frac{\pi}{3} = \frac{2\pi}{3}$.
The area of the segment of Circle 2 to the right of the chord ($x \ge 1/2$) is given by $\frac{1}{2}r^2(\theta - \sin\theta) = \frac{1}{2}(1)^2(\frac{2\pi}{3} - \sin(\frac{2\pi}{3})) = \frac{1}{2}(\frac{2\pi}{3} - \frac{\sqrt{3}}{2}) = \frac{\pi}{3} - \frac{\sqrt{3}}{4}$.
For Circle 1 ($(x-1)^2 + y^2 = 1$), centered at $(1,0)$ with radius $r=1$, the chord is $x=1/2$. The distance from the center to the chord is $d = |1 - 1/2| = 1/2$. The angle $\phi$ subtended by the chord at the center is $2 \times \cos^{-1}(d/r) = 2 \times \cos^{-1}(1/2) = 2 \times \frac{\pi}{3} = \frac{2\pi}{3}$.
The area of the segment of Circle 1 to the left of the chord ($x \le 1/2$) is given by $\frac{1}{2}r^2(\phi - \sin\phi) = \frac{1}{2}(1)^2(\frac{2\pi}{3} - \sin(\frac{2\pi}{3})) = \frac{1}{2}(\frac{2\pi}{3} - \frac{\sqrt{3}}{2}) = \frac{\pi}{3} - \frac{\sqrt{3}}{4}$.
The total area of the region bounded by the two circles is the sum of the areas of these two segments:
Total Area $A = (\frac{\pi}{3} - \frac{\sqrt{3}}{4}) + (\frac{\pi}{3} - \frac{\sqrt{3}}{4}) = \frac{2\pi}{3} - \frac{2\sqrt{3}}{4} = \frac{2\pi}{3} - \frac{\sqrt{3}}{2}$.
Final Answer:
The area bounded by the curves $(x – 1)^2 + y^2 = 1$ and $x^2 + y^2 = 1$ is $\frac{2\pi}{3} - \frac{\sqrt{3}}{2}$ square units.
Question 3. Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3.
Answer:
Given:
The region is bounded by the curves and lines:
1. Curve: $y = x^2 + 2$
2. Line: $y = x$
3. Line: $x = 0$ (y-axis)
4. Line: $x = 3$
To Find:
The area of the region bounded by the given curves and lines.
Solution:
The given curves and lines are $y = x^2 + 2$, $y = x$, $x = 0$, and $x = 3$.
The curve $y = x^2 + 2$ is a parabola opening upwards with its vertex at $(0, 2)$.
The line $y = x$ passes through the origin with a slope of 1.
The lines $x=0$ and $x=3$ are vertical lines that define the left and right boundaries of the region.
We need to determine which curve is above the other in the interval $[0, 3]$. Let's compare the values of $y$ for $y = x^2 + 2$ and $y = x$ in this interval.
Consider the difference $(x^2 + 2) - x = x^2 - x + 2$.
To check if this difference is positive or negative, we can analyze the quadratic $f(x) = x^2 - x + 2$. The discriminant is $\Delta = (-1)^2 - 4(1)(2) = 1 - 8 = -7$. Since the discriminant is negative ($\Delta < 0$) and the coefficient of $x^2$ is positive (1 > 0), the quadratic $x^2 - x + 2$ is always positive for all real values of $x$.
Therefore, $x^2 + 2 > x$ for all $x$. This means the curve $y = x^2 + 2$ is always above the line $y = x$ throughout the interval $[0, 3]$.
The area of the region bounded by the curves and lines is given by the integral of the difference between the upper curve ($y = x^2 + 2$) and the lower curve ($y = x$) from $x = 0$ to $x = 3$.
Area $A = \int\limits_{0}^{3} ((x^2 + 2) - x) \$ dx$
$A = \int\limits_{0}^{3} (x^2 - x + 2) \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^{2+1}}{2+1} - \frac{x^{1+1}}{1+1} + 2x\right]_{0}^{3}$
$A = \left[\frac{x^3}{3} - \frac{x^2}{2} + 2x\right]_{0}^{3}$
Substitute the upper limit $x=3$:
$\left(\frac{3^3}{3} - \frac{3^2}{2} + 2(3)\right) = \left(\frac{27}{3} - \frac{9}{2} + 6\right) = \left(9 - \frac{9}{2} + 6\right)$
$= \left(15 - \frac{9}{2}\right) = \left(\frac{30}{2} - \frac{9}{2}\right) = \frac{21}{2}$
Substitute the lower limit $x=0$:
$\left(\frac{0^3}{3} - \frac{0^2}{2} + 2(0)\right) = (0 - 0 + 0) = 0$
Evaluate the definite integral:
$A = \frac{21}{2} - 0 = \frac{21}{2}$
Final Answer:
The area of the region bounded by the curves $y = x^2 + 2$, $y = x$, $x = 0$, and $x = 3$ is $\frac{21}{2}$ square units.
Question 4. Using integration find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
Answer:
Given:
The vertices of the triangle are A(-1, 0), B(1, 3), and C(3, 2).
To Find:
The area of the region bounded by the triangle using integration.
Solution:
To find the area of the triangle using integration, we first find the equations of the lines joining the vertices.
Equation of line AB:
Points A(-1, 0) and B(1, 3).
The slope $m_{AB} = \frac{3 - 0}{1 - (-1)} = \frac{3}{2}$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with A(-1, 0):
$y - 0 = \frac{3}{2}(x - (-1))$
$y = \frac{3}{2}(x + 1)$
$y = \frac{3}{2}x + \frac{3}{2}$
Equation of line BC:
Points B(1, 3) and C(3, 2).
The slope $m_{BC} = \frac{2 - 3}{3 - 1} = \frac{-1}{2}$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with B(1, 3):
$y - 3 = -\frac{1}{2}(x - 1)$
$y = -\frac{1}{2}x + \frac{1}{2} + 3$
$y = -\frac{1}{2}x + \frac{7}{2}$
Equation of line AC:
Points A(-1, 0) and C(3, 2).
The slope $m_{AC} = \frac{2 - 0}{3 - (-1)} = \frac{2}{4} = \frac{1}{2}$.
Using the point-slope form $y - y_1 = m(x - x_1)$ with A(-1, 0):
$y - 0 = \frac{1}{2}(x - (-1))$
$y = \frac{1}{2}x + \frac{1}{2}$
The triangle ABC lies above the line AC and is bounded by the line segments AB (from x=-1 to x=1) and BC (from x=1 to x=3) as the upper boundary, and the line segment AC (from x=-1 to x=3) as the lower boundary.
The area of the triangle can be calculated by integrating the difference between the upper boundary curves and the lower boundary curve over the relevant x-intervals.
The x-coordinates of the vertices are -1, 1, and 3. We split the integral at x=1.
Area $A = \int\limits_{-1}^{1} (\text{y}_{\text{AB}} - \text{y}_{\text{AC}}) \$ dx + \int\limits_{1}^{3} (\text{y}_{\text{BC}} - \text{y}_{\text{AC}}) \$ dx$
$A = \int\limits_{-1}^{1} \left(\left(\frac{3}{2}x + \frac{3}{2}\right) - \left(\frac{1}{2}x + \frac{1}{2}\right)\right) \$ dx + \int\limits_{1}^{3} \left(\left(-\frac{1}{2}x + \frac{7}{2}\right) - \left(\frac{1}{2}x + \frac{1}{2}\right)\right) \$ dx$
Simplify the integrands:
$(\frac{3}{2}x + \frac{3}{2}) - (\frac{1}{2}x + \frac{1}{2}) = (\frac{3}{2} - \frac{1}{2})x + (\frac{3}{2} - \frac{1}{2}) = \frac{2}{2}x + \frac{2}{2} = x + 1$
$(-\frac{1}{2}x + \frac{7}{2}) - (\frac{1}{2}x + \frac{1}{2}) = (-\frac{1}{2} - \frac{1}{2})x + (\frac{7}{2} - \frac{1}{2}) = -\frac{2}{2}x + \frac{6}{2} = -x + 3$
The area integral becomes:
$A = \int\limits_{-1}^{1} (x + 1) \$ dx + \int\limits_{1}^{3} (-x + 3) \$ dx$
Evaluate the first integral:
$\int\limits_{-1}^{1} (x + 1) \$ dx = \left[\frac{x^2}{2} + x\right]_{-1}^{1}$
$= \left(\frac{1^2}{2} + 1\right) - \left(\frac{(-1)^2}{2} + (-1)\right)$
$= \left(\frac{1}{2} + 1\right) - \left(\frac{1}{2} - 1\right)$
$= \frac{3}{2} - (-\frac{1}{2}) = \frac{3}{2} + \frac{1}{2} = \frac{4}{2} = 2$
Evaluate the second integral:
$\int\limits_{1}^{3} (-x + 3) \$ dx = \left[-\frac{x^2}{2} + 3x\right]_{1}^{3}$
$= \left(-\frac{3^2}{2} + 3(3)\right) - \left(-\frac{1^2}{2} + 3(1)\right)$
$= \left(-\frac{9}{2} + 9\right) - \left(-\frac{1}{2} + 3\right)$
$= \left(-\frac{9}{2} + \frac{18}{2}\right) - \left(-\frac{1}{2} + \frac{6}{2}\right)$
$= \frac{9}{2} - \frac{5}{2} = \frac{4}{2} = 2$
Total Area $A = 2 + 2 = 4$
Final Answer:
The area of the region bounded by the triangle with vertices (– 1, 0), (1, 3), and (3, 2) is 4 square units.
Question 5. Using integration find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Answer:
Given:
The sides of the triangular region have the equations:
1. $y = 2x + 1$
2. $y = 3x + 1$
3. $x = 4$
To Find:
The area of the triangular region bounded by the given lines using integration.
Solution:
First, we find the vertices of the triangle by finding the intersection points of the given lines.
Intersection of $y = 2x + 1$ and $y = 3x + 1$:
$2x + 1 = 3x + 1$
$0 = x$
Substitute $x=0$ into $y = 2x + 1$: $y = 2(0) + 1 = 1$.
The first vertex is $(0, 1)$.
Intersection of $y = 2x + 1$ and $x = 4$:
Substitute $x=4$ into $y = 2x + 1$: $y = 2(4) + 1 = 8 + 1 = 9$.
The second vertex is $(4, 9)$.
Intersection of $y = 3x + 1$ and $x = 4$:
Substitute $x=4$ into $y = 3x + 1$: $y = 3(4) + 1 = 12 + 1 = 13$.
The third vertex is $(4, 13)$.
The vertices of the triangle are $(0, 1)$, $(4, 9)$, and $(4, 13)$.
The region is bounded by the line segments connecting these vertices. The x-coordinates of the vertices range from 0 to 4. The vertical line $x=4$ forms one side of the triangle.
For $0 < x < 4$, let's compare the values of $y$ for the lines $y = 2x + 1$ and $y = 3x + 1$.
The line $y = 3x + 1$ has a greater slope (3) than the line $y = 2x + 1$ (2). Since they intersect at $x=0$, for $x > 0$, the line with the greater slope will be above the line with the smaller slope.
Thus, for $x > 0$, $3x + 1 > 2x + 1$.
The region bounded by the three lines is bounded below by the line $y = 2x + 1$ and bounded above by the line $y = 3x + 1$, from $x=0$ to $x=4$.
The area of the triangular region is given by the integral of the difference between the upper curve ($y = 3x + 1$) and the lower curve ($y = 2x + 1$) from $x = 0$ to $x = 4$.
Area $A = \int\limits_{0}^{4} ((3x + 1) - (2x + 1)) \$ dx$
$A = \int\limits_{0}^{4} (3x + 1 - 2x - 1) \$ dx$
$A = \int\limits_{0}^{4} x \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^2}{2}\right]_{0}^{4}$
Substitute the upper limit $x=4$:
$\frac{4^2}{2} = \frac{16}{2} = 8$
Substitute the lower limit $x=0$:
$\frac{0^2}{2} = 0$
Evaluate the definite integral:
$A = 8 - 0 = 8$
Final Answer:
The area of the triangular region whose sides have the equations $y = 2x + 1$, $y = 3x + 1$, and $x = 4$ is 8 square units.
Choose the correct answer in the following exercises 6 and 7.
Question 6. Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
Answer:
Given:
The bounding curves are the circle $x^2 + y^2 = 4$ and the line $x + y = 2$.
To Find:
The area of the smaller region enclosed by the circle and the line.
Solution:
The equation of the circle is $x^2 + y^2 = 4$, which is centered at the origin $(0,0)$ with radius $r = \sqrt{4} = 2$.
The equation of the line is $x + y = 2$, which can be written as $y = 2 - x$.
To find the points of intersection of the circle and the line, substitute $y = 2 - x$ into the equation of the circle:
$x^2 + (2 - x)^2 = 4$
$x^2 + (4 - 4x + x^2) = 4$
$2x^2 - 4x + 4 = 4$
$2x^2 - 4x = 0$
$2x(x - 2) = 0$
This gives the x-coordinates of the intersection points: $x = 0$ and $x = 2$.
Find the corresponding y-coordinates using $y = 2 - x$:
If $x = 0$, $y = 2 - 0 = 2$. Intersection point is $(0, 2)$.
If $x = 2$, $y = 2 - 2 = 0$. Intersection point is $(2, 0)$.
The line $x + y = 2$ cuts the circle into two parts. The smaller area enclosed is the region bounded above by the circle ($y = \sqrt{4 - x^2}$) and bounded below by the line ($y = 2 - x$), between the x-coordinates of the intersection points ($x=0$ and $x=2$).
The area of this region is given by the integral of the difference between the upper curve and the lower curve from $x = 0$ to $x = 2$.
Area $A = \int\limits_{0}^{2} (\sqrt{4 - x^2} - (2 - x)) \$ dx$
$A = \int\limits_{0}^{2} \sqrt{4 - x^2} \$ dx - \int\limits_{0}^{2} (2 - x) \$ dx$
Evaluate the first integral $\int\limits_{0}^{2} \sqrt{4 - x^2} \$ dx$ using the formula $\int \sqrt{a^2 - x^2} \$ dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$, with $a=2$.
$\int\limits_{0}^{2} \sqrt{4 - x^2} \$ dx = \left[\frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
$= \left[\frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right)\right]_{0}^{2}$
$= \left(\frac{2}{2}\sqrt{4 - 2^2} + 2\sin^{-1}\left(\frac{2}{2}\right)\right) - \left(\frac{0}{2}\sqrt{4 - 0^2} + 2\sin^{-1}\left(\frac{0}{2}\right)\right)$
$= (1\sqrt{0} + 2\sin^{-1}(1)) - (0 + 2\sin^{-1}(0))$
$= (0 + 2 \times \frac{\pi}{2}) - (0 + 0) = \pi$
Evaluate the second integral $\int\limits_{0}^{2} (2 - x) \$ dx$:
$\int\limits_{0}^{2} (2 - x) \$ dx = \left[2x - \frac{x^2}{2}\right]_{0}^{2}$
$= \left(2(2) - \frac{2^2}{2}\right) - \left(2(0) - \frac{0^2}{2}\right)$
$= (4 - 2) - (0) = 2$
The total area of the smaller region is the difference between these two integrals:
$A = \pi - 2$
Alternate Method:
The region bounded by the circle $x^2+y^2=4$ and the line $x+y=2$ can be seen as the area of the circular sector corresponding to the arc above the line, minus the area of the triangle formed by the origin and the intersection points $(0,2)$ and $(2,0)$. However, direct sector calculation is for sectors from the center. A simpler approach is to consider the area of the quarter circle in the first quadrant (bounded by the x-axis, y-axis, and the circle arc) and subtract the area of the triangle formed by the points $(0,0)$, $(2,0)$, and $(0,2)$.
The circle $x^2+y^2=4$ has radius $r=2$. The area of the quarter circle in the first quadrant is $\frac{1}{4}\pi r^2 = \frac{1}{4}\pi (2)^2 = \pi$.
The line $x+y=2$ passes through $(2,0)$ and $(0,2)$. The triangle formed by the origin $(0,0)$ and these two points is a right-angled triangle with base 2 (along the x-axis) and height 2 (along the y-axis).
Area of triangle OAB $= \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 2 \times 2 = 2$.
The area of the smaller segment is the area of the quarter circle minus the area of this triangle:
Area = Area (Quarter Circle) - Area (Triangle OAB) = $\pi - 2$.
Final Answer:
The area of the smaller region enclosed by the circle $x^2 + y^2 = 4$ and the line $x + y = 2$ is $\pi - 2$ square units.
Comparing with the given options, the correct answer is (B) $\pi - 2$.
Question 7. Area lying between the curves y2 = 4x and y = 2x is
(A) $\frac{2}{3}$
(B) $\frac{1}{3}$
(C) $\frac{1}{4}$
(D) $\frac{3}{4}$
Answer:
Given:
The bounding curves are $y^2 = 4x$ and $y = 2x$.
To Find:
The area of the region bounded by the given curves.
Solution:
The given curves are the parabola $y^2 = 4x$ and the line $y = 2x$.
To find the points of intersection, substitute $y = 2x$ into the equation of the parabola:
$(2x)^2 = 4x$
$4x^2 = 4x$
$4x^2 - 4x = 0$
$4x(x - 1) = 0$
The intersection points occur at $x = 0$ and $x = 1$.
When $x = 0$, $y = 2(0) = 0$. Intersection point is $(0, 0)$.
When $x = 1$, $y = 2(1) = 2$. Intersection point is $(1, 2)$.
The region bounded by the curves is between $x=0$ and $x=1$.
For $x \in (0, 1)$, the parabola $y^2=4x$ corresponds to $y=\sqrt{4x}=2\sqrt{x}$ (taking the positive root since the line $y=2x$ is in the first quadrant for $x \in (0,1)$).
To determine which curve is above the other, let's check $x = 1/4$:
For $y = 2\sqrt{x}$, $y = 2\sqrt{1/4} = 2 \times \frac{1}{2} = 1$.
For $y = 2x$, $y = 2 \times \frac{1}{4} = \frac{1}{2}$.
Since $1 > \frac{1}{2}$, the curve $y = 2\sqrt{x}$ is above the line $y = 2x$ in the interval $(0, 1)$.
The area of the bounded region is given by the integral of the difference between the upper curve ($y = 2\sqrt{x}$) and the lower curve ($y = 2x$) from $x = 0$ to $x = 1$.
Area $A = \int\limits_{0}^{1} (2\sqrt{x} - 2x) \$ dx$
$A = \int\limits_{0}^{1} (2x^{1/2} - 2x) \$ dx$
Now, we evaluate the integral:
$A = \left[2 \frac{x^{3/2}}{3/2} - 2 \frac{x^2}{2}\right]_{0}^{1}$
$A = \left[\frac{4}{3}x^{3/2} - x^2\right]_{0}^{1}$
Substitute the upper limit $x=1$:
$\frac{4}{3}(1)^{3/2} - (1)^2 = \frac{4}{3} - 1 = \frac{1}{3}$
Substitute the lower limit $x=0$:
$\frac{4}{3}(0)^{3/2} - (0)^2 = 0$
Evaluate the definite integral:
$A = \frac{1}{3} - 0 = \frac{1}{3}$
Final Answer:
The area lying between the curves $y^2 = 4x$ and $y = 2x$ is $\frac{1}{3}$ square units.
Comparing with the given options, the correct answer is (B) $\frac{1}{3}$.
Example 11 to 15 - Miscellaneous Examples
Example 11: Find the area of the parabola y2 = 4ax bounded by its latus rectum.
Answer:
Given:
The curve is the parabola $y^2 = 4ax$.
The boundary is the latus rectum of the parabola.
To Find:
The area of the region bounded by the parabola and its latus rectum.
Solution:
The equation of the parabola is $y^2 = 4ax$. This parabola opens to the right and is symmetric about the x-axis. Its vertex is at the origin $(0,0)$.
The focus of the parabola $y^2 = 4ax$ is at the point $(a, 0)$.
The latus rectum is a line segment perpendicular to the axis of the parabola (the x-axis) passing through the focus. Thus, the equation of the line containing the latus rectum is $x = a$.
To find the points of intersection of the parabola $y^2 = 4x$ and the line $x=a$, substitute $x=a$ into the parabola equation:
$y^2 = 4a(a) = 4a^2$
$y = \pm \sqrt{4a^2} = \pm 2a$
The intersection points are $(a, 2a)$ and $(a, -2a)$. These are the endpoints of the latus rectum.
The region bounded by the parabola $y^2 = 4ax$ and the latus rectum $x=a$ is the area between the vertex $(x=0)$ and the line $x=a$. This region is enclosed by the upper half of the parabola $y = \sqrt{4ax} = 2\sqrt{ax}$ (for $y \ge 0$) and the lower half $y = -2\sqrt{ax}$ (for $y < 0$), bounded by the line $x=a$.
Due to the symmetry of the parabola about the x-axis, the total area is twice the area of the region in the first quadrant bounded by the curve $y = 2\sqrt{ax}$, the x-axis ($y=0$), and the line $x=a$.
The area in the first quadrant is given by the integral of $y = 2\sqrt{ax}$ with respect to $x$ from $x=0$ to $x=a$.
Area $A = 2 \times \int\limits_{0}^{a} 2\sqrt{ax} \$ dx$
$A = 4\sqrt{a} \int\limits_{0}^{a} \sqrt{x} \$ dx$
$A = 4\sqrt{a} \int\limits_{0}^{a} x^{1/2} \$ dx$
Now, we evaluate the integral:
The antiderivative of $x^{1/2}$ is $\frac{x^{1/2 + 1}}{1/2 + 1} = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}$.
$A = 4\sqrt{a} \left[\frac{2}{3}x^{3/2}\right]_{0}^{a}$
$A = \frac{8}{3}\sqrt{a} \left[x^{3/2}\right]_{0}^{a}$
Substitute the upper limit $x=a$:
$a^{3/2}$
Substitute the lower limit $x=0$:
$0^{3/2} = 0$
Evaluate the definite integral:
$A = \frac{8}{3}\sqrt{a} (a^{3/2} - 0) = \frac{8}{3} a^{1/2} a^{3/2}$
$A = \frac{8}{3} a^{(1/2 + 3/2)} = \frac{8}{3} a^{4/2} = \frac{8}{3} a^2$
Final Answer:
The area of the parabola $y^2 = 4ax$ bounded by its latus rectum is $\frac{8}{3} a^2$ square units.
Example 12: Find the area of the region bounded by the line y = 3x + 2, the x-axis and the ordinates x = –1 and x = 1.
Answer:
Given:
The bounding lines are:
1. Line: $y = 3x + 2$
2. The x-axis ($y = 0$)
3. Ordinate: $x = -1$
4. Ordinate: $x = 1$
To Find:
The area of the region bounded by the given lines and the x-axis.
Solution:
The given region is bounded by the line $y = 3x + 2$, the x-axis ($y=0$), and the vertical lines $x = -1$ and $x = 1$.
First, find where the line $y = 3x + 2$ intersects the x-axis by setting $y = 0$:
$3x + 2 = 0$
$3x = -2$
$x = -\frac{2}{3}$
The line intersects the x-axis at $x = -\frac{2}{3}$. This x-value lies within the interval $[-1, 1]$.
The region is divided into two parts by the x-axis in the given interval:
Part 1: From $x = -1$ to $x = -\frac{2}{3}$, the line $y = 3x + 2$ is below the x-axis (i.e., $y < 0$). The area is $\int\limits_{-1}^{-2/3} |3x + 2| \$ dx = \int\limits_{-1}^{-2/3} -(3x + 2) \$ dx = \int\limits_{-1}^{-2/3} (-3x - 2) \$ dx$.
Part 2: From $x = -\frac{2}{3}$ to $x = 1$, the line $y = 3x + 2$ is above the x-axis (i.e., $y > 0$). The area is $\int\limits_{-2/3}^{1} |3x + 2| \$ dx = \int\limits_{-2/3}^{1} (3x + 2) \$ dx$.
The total area is the sum of the areas of these two parts:
Area $A = \int\limits_{-1}^{-2/3} (-3x - 2) \$ dx + \int\limits_{-2/3}^{1} (3x + 2) \$ dx$
Evaluate the first integral:
$\int\limits_{-1}^{-2/3} (-3x - 2) \$ dx = \left[-\frac{3x^2}{2} - 2x\right]_{-1}^{-2/3}$
$= \left(-\frac{3}{2}\left(-\frac{2}{3}\right)^2 - 2\left(-\frac{2}{3}\right)\right) - \left(-\frac{3}{2}(-1)^2 - 2(-1)\right)$
$= \left(-\frac{3}{2}\left(\frac{4}{9}\right) + \frac{4}{3}\right) - \left(-\frac{3}{2} + 2\right)$
$= \left(-\frac{12}{18} + \frac{4}{3}\right) - \left(-\frac{3}{2} + \frac{4}{2}\right)$
$= \left(-\frac{2}{3} + \frac{4}{3}\right) - \left(\frac{1}{2}\right) = \frac{2}{3} - \frac{1}{2} = \frac{4 - 3}{6} = \frac{1}{6}$
Evaluate the second integral:
$\int\limits_{-2/3}^{1} (3x + 2) \$ dx = \left[\frac{3x^2}{2} + 2x\right]_{-2/3}^{1}$
$= \left(\frac{3}{2}(1)^2 + 2(1)\right) - \left(\frac{3}{2}\left(-\frac{2}{3}\right)^2 + 2\left(-\frac{2}{3}\right)\right)$
$= \left(\frac{3}{2} + 2\right) - \left(\frac{3}{2}\left(\frac{4}{9}\right) - \frac{4}{3}\right)$
$= \left(\frac{3}{2} + \frac{4}{2}\right) - \left(\frac{12}{18} - \frac{4}{3}\right)$
$= \frac{7}{2} - \left(\frac{2}{3} - \frac{4}{3}\right) = \frac{7}{2} - \left(-\frac{2}{3}\right) = \frac{7}{2} + \frac{2}{3} = \frac{21 + 4}{6} = \frac{25}{6}$
The total area is the sum of the areas of the two parts:
$A = \frac{1}{6} + \frac{25}{6} = \frac{26}{6}$
Simplify the fraction:
$A = \frac{\cancel{26}^{13}}{\cancel{6}_{3}} = \frac{13}{3}$
Final Answer:
The area of the region bounded by the line $y = 3x + 2$, the x-axis and the ordinates $x = –1$ and $x = 1$ is $\frac{13}{3}$ square units.
Example 13: Find the area bounded by the curve y = cos x between x = 0 and x = 2π.
Answer:
Given:
The curve is $y = \cos x$.
The interval is from $x = 0$ to $x = 2\pi$.
To Find:
The area bounded by the curve, the x-axis, and the lines $x = 0$ and $x = 2\pi$.
Solution:
The area bounded by a curve $y = f(x)$ and the x-axis from $x=a$ to $x=b$ is given by $\int\limits_{a}^{b} |f(x)| \$ dx$.
In this case, we need to find the area $\int\limits_{0}^{2\pi} |\cos x| \$ dx$.
We need to determine the intervals where $\cos x$ is positive and where it is negative in the interval $[0, 2\pi]$.
$\cos x = 0$ at $x = \frac{\pi}{2}$ and $x = \frac{3\pi}{2}$ in the interval $[0, 2\pi]$.
The intervals are $[0, \frac{\pi}{2}]$, $[\frac{\pi}{2}, \frac{3\pi}{2}]$, and $[\frac{3\pi}{2}, 2\pi]$.
In $[0, \frac{\pi}{2}]$, $\cos x \ge 0$.
In $[\frac{\pi}{2}, \frac{3\pi}{2}]$, $\cos x \le 0$.
In $[\frac{3\pi}{2}, 2\pi]$, $\cos x \ge 0$.
So, the total area is the sum of the absolute values of the integrals over these intervals:
$A = \int\limits_{0}^{2\pi} |\cos x| \$ dx = \int\limits_{0}^{\pi/2} \cos x \$ dx + \int\limits_{\pi/2}^{3\pi/2} |\cos x| \$ dx + \int\limits_{3\pi/2}^{2\pi} \cos x \$ dx$
$A = \int\limits_{0}^{\pi/2} \cos x \$ dx + \int\limits_{\pi/2}^{3\pi/2} (-\cos x) \$ dx + \int\limits_{3\pi/2}^{2\pi} \cos x \$ dx$
Now, evaluate each integral:
$\int \cos x \$ dx = \sin x$
$\int\limits_{0}^{\pi/2} \cos x \$ dx = [\sin x]_{0}^{\pi/2} = \sin\left(\frac{\pi}{2}\right) - \sin(0) = 1 - 0 = 1$
$\int\limits_{\pi/2}^{3\pi/2} (-\cos x) \$ dx = [-\sin x]_{\pi/2}^{3\pi/2} = (-\sin\left(\frac{3\pi}{2}\right)) - (-\sin\left(\frac{\pi}{2}\right)) = (-(-1)) - (-(1)) = 1 + 1 = 2$
$\int\limits_{3\pi/2}^{2\pi} \cos x \$ dx = [\sin x]_{3\pi/2}^{2\pi} = \sin(2\pi) - \sin\left(\frac{3\pi}{2}\right) = 0 - (-1) = 1$
Add the values of the integrals to find the total area:
$A = 1 + 2 + 1 = 4$
Final Answer:
The area bounded by the curve $y = \cos x$ between $x = 0$ and $x = 2\pi$ is 4 square units.
Example 14: Prove that the curves y2 = 4x and x2 = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Answer:
Given:
The curves are the parabola $y^2 = 4x$ and the parabola $x^2 = 4y$.
The square is bounded by the lines $x = 0$, $x = 4$, $y = 4$, and $y = 0$.
To Prove:
The area of the square bounded by $x=0, x=4, y=4, y=0$ is divided into three equal parts by the curves $y^2 = 4x$ and $x^2 = 4y$.
Solution:
The square region is defined by $0 \le x \le 4$ and $0 \le y \le 4$. The total area of this square is $4 \times 4 = 16$ square units.
The equations of the curves are $y^2 = 4x$ and $x^2 = 4y$. Both are parabolas opening along the positive x and y axes, respectively, with vertices at the origin $(0,0)$.
To find the intersection points of the two parabolas, substitute $y = \frac{x^2}{4}$ (from $x^2 = 4y$) into $y^2 = 4x$:
$\left(\frac{x^2}{4}\right)^2 = 4x$
$\frac{x^4}{16} = 4x$
$x^4 = 64x$
$x^4 - 64x = 0$
$x(x^3 - 64) = 0$
The real solutions are $x = 0$ or $x^3 = 64$, which gives $x = 4$.
For $x=0$, $y = 0^2/4 = 0$. Intersection point: $(0,0)$.
For $x=4$, $y = 4^2/4 = 16/4 = 4$. Intersection point: $(4,4)$.
The two parabolas intersect at the vertices $(0,0)$ and $(4,4)$ of the square.
The region of the square is divided into three parts by these two curves:
Part 1 ($R_1$): The region bounded by the parabola $y = \frac{x^2}{4}$ and the x-axis ($y=0$), from $x=0$ to $x=4$. This is the region below the parabola $y=x^2/4$ within the square.
Part 2 ($R_2$): The region bounded by the parabola $x = \frac{y^2}{4}$ (from $y^2=4x$) and the y-axis ($x=0$), from $y=0$ to $y=4$. This is the region to the left of the parabola $x=y^2/4$ within the square.
Part 3 ($R_3$): The region bounded by the two parabolas, $y = \frac{x^2}{4}$ below and $y = \sqrt{4x} = 2\sqrt{x}$ above, from $x=0$ to $x=4$. This is the central region between the two curves.
Let's calculate the area of each part using integration.
Area of Region 1 ($A_1$):
This is the area under the curve $y = \frac{x^2}{4}$ from $x=0$ to $x=4$.
$A_1 = \int\limits_{0}^{4} \frac{x^2}{4} \$ dx$
$A_1 = \frac{1}{4} \int\limits_{0}^{4} x^2 \$ dx$
$A_1 = \frac{1}{4} \left[\frac{x^3}{3}\right]_{0}^{4}$
$A_1 = \frac{1}{12} [4^3 - 0^3] = \frac{1}{12} (64) = \frac{64}{12} = \frac{16}{3}$ square units.
Area of Region 2 ($A_2$):
This is the area to the left of the curve $x = \frac{y^2}{4}$ from $y=0$ to $y=4$. We integrate with respect to y.
$A_2 = \int\limits_{0}^{4} \frac{y^2}{4} \$ dy$
$A_2 = \frac{1}{4} \int\limits_{0}^{4} y^2 \$ dy$
$A_2 = \frac{1}{4} \left[\frac{y^3}{3}\right]_{0}^{4}$
$A_2 = \frac{1}{12} [4^3 - 0^3] = \frac{1}{12} (64) = \frac{64}{12} = \frac{16}{3}$ square units.
Area of Region 3 ($A_3$):
This is the area between the two parabolas from $x=0$ to $x=4$. The upper curve is $y = 2\sqrt{x}$ and the lower curve is $y = \frac{x^2}{4}$ in the interval $[0, 4]$.
$A_3 = \int\limits_{0}^{4} \left(2\sqrt{x} - \frac{x^2}{4}\right) \$ dx$
$A_3 = \int\limits_{0}^{4} 2x^{1/2} \$ dx - \int\limits_{0}^{4} \frac{x^2}{4} \$ dx$
$A_3 = \left[2 \frac{x^{3/2}}{3/2}\right]_{0}^{4} - \left[\frac{x^3}{12}\right]_{0}^{4}$
$A_3 = \left[\frac{4}{3}x^{3/2}\right]_{0}^{4} - \left[\frac{x^3}{12}\right]_{0}^{4}$
$A_3 = \left(\frac{4}{3}(4)^{3/2} - \frac{4}{3}(0)^{3/2}\right) - \left(\frac{4^3}{12} - \frac{0^3}{12}\right)$
$A_3 = \left(\frac{4}{3}(8) - 0\right) - \left(\frac{64}{12} - 0\right)$
$A_3 = \frac{32}{3} - \frac{16}{3} = \frac{16}{3}$ square units.
The three areas are $A_1 = \frac{16}{3}$, $A_2 = \frac{16}{3}$, and $A_3 = \frac{16}{3}$.
The total area of the square is $16$. One-third of the total area is $\frac{16}{3}$.
Since $A_1 = A_2 = A_3 = \frac{16}{3} = \frac{1}{3} \times 16$, the three areas are equal and each is equal to one-third of the total area of the square.
Thus, the curves $y^2 = 4x$ and $x^2 = 4y$ divide the area of the square bounded by $x = 0, x = 4, y = 4$ and $y = 0$ into three equal parts.
Conclusion:
The areas of the three regions are $A_1 = \frac{16}{3}$, $A_2 = \frac{16}{3}$, and $A_3 = \frac{16}{3}$, which are equal. The total area is $A_1 + A_2 + A_3 = \frac{16}{3} + \frac{16}{3} + \frac{16}{3} = \frac{48}{3} = 16$. The area of the square is $4 \times 4 = 16$. Therefore, the area is divided into three equal parts.
Example 15: Find the area of the region
{(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2}
Answer:
Given:
The region is defined by the set {(x, y) : 0 $\le$ y $\le$ x$^2$ + 1, 0 $\le$ y $\le$ x + 1, 0 $\le$ x $\le$ 2}.
To Find:
The area of the given region.
Solution:
The region is bounded by the x-axis ($y=0$), the curve $y = x^2 + 1$, the line $y = x + 1$, and the vertical lines $x = 0$ and $x = 2$.
The condition $0 \le y \le x^2 + 1$ means the region is below the curve $y = x^2 + 1$ and above or on the x-axis.
The condition $0 \le y \le x + 1$ means the region is below the line $y = x + 1$ and above or on the x-axis.
The condition $0 \le x \le 2$ defines the interval for x.
The region is therefore described by $0 \le x \le 2$ and $0 \le y \le \min(x^2 + 1, x + 1)$.
We need to find the points where the two upper bounding curves intersect by setting $y = x^2 + 1$ equal to $y = x + 1$:
$x^2 + 1 = x + 1$
$x^2 - x = 0$
$x(x - 1) = 0$
The intersection points are $x = 0$ and $x = 1$. These points lie within the given interval $0 \le x \le 2$.
We need to determine which function is smaller in the subintervals $[0, 1]$ and $[1, 2]$.
Consider $f(x) = x^2 + 1$ and $g(x) = x + 1$.
In the interval $[0, 1]$, let's check $x = 0.5$. $f(0.5) = (0.5)^2 + 1 = 0.25 + 1 = 1.25$, $g(0.5) = 0.5 + 1 = 1.5$. Since $1.25 \le 1.5$, we have $x^2 + 1 \le x + 1$ for $x \in [0, 1]$.
In the interval $[1, 2]$, let's check $x = 1.5$. $f(1.5) = (1.5)^2 + 1 = 2.25 + 1 = 3.25$, $g(1.5) = 1.5 + 1 = 2.5$. Since $2.5 \le 3.25$, we have $x + 1 \le x^2 + 1$ for $x \in [1, 2]$.
So, the area is calculated by integrating $\min(x^2+1, x+1)$ from $x=0$ to $x=2$. This requires splitting the integral at the intersection point $x=1$:
Area $A = \int\limits_{0}^{1} (x^2 + 1) \$ dx + \int\limits_{1}^{2} (x + 1) \$ dx$
Evaluate the first integral:
$\int\limits_{0}^{1} (x^2 + 1) \$ dx = \left[\frac{x^3}{3} + x\right]_{0}^{1}$
$= \left(\frac{1^3}{3} + 1\right) - \left(\frac{0^3}{3} + 0\right)$
$= \left(\frac{1}{3} + \frac{3}{3}\right) - 0 = \frac{4}{3}$
Evaluate the second integral:
$\int\limits_{1}^{2} (x + 1) \$ dx = \left[\frac{x^2}{2} + x\right]_{1}^{2}$
$= \left(\frac{2^2}{2} + 2\right) - \left(\frac{1^2}{2} + 1\right)$
$= \left(\frac{4}{2} + 2\right) - \left(\frac{1}{2} + \frac{2}{2}\right)$
$= (2 + 2) - \frac{3}{2} = 4 - \frac{3}{2} = \frac{8}{2} - \frac{3}{2} = \frac{5}{2}$
The total area is the sum of the areas of the two parts:
$A = \frac{4}{3} + \frac{5}{2}$
To add these fractions, find a common denominator, which is 6.
$A = \frac{4}{3} \times \frac{2}{2} + \frac{5}{2} \times \frac{3}{3}$
$A = \frac{8}{6} + \frac{15}{6}$
$A = \frac{8 + 15}{6} = \frac{23}{6}$
Final Answer:
The area of the region {(x, y) : 0 $\le$ y $\le$ x$^2$ + 1, 0 $\le$ y $\le$ x + 1, 0 $\le$ x $\le$ 2} is $\frac{23}{6}$ square units.
Miscellaneous Exercise on Chapter 8
Question 1. Find the area under the given curves and given lines:
(i) y = x2 , x = 1, x = 2 and x-axis
(ii) y = x4 , x = 1, x = 5 and x-axis
Answer:
(i)
Given:
The bounding curves and lines are:
1. Curve: $y = x^2$
2. Line: $x = 1$
3. Line: $x = 2$
4. The x-axis ($y = 0$)
To Find:
The area of the region bounded by the given curve and lines.
Solution:
The given curve is $y = x^2$, which is a parabola opening upwards. The lines are $x=1$ and $x=2$, which are vertical lines. The x-axis is $y=0$.
In the interval $[1, 2]$, the function $y = x^2$ is non-negative ($x^2 \ge 0$).
The area of the region bounded by the curve $y = x^2$, the lines $x = 1$, $x = 2$, and the x-axis is given by the definite integral of $y = x^2$ from $x=1$ to $x=2$.
Area $A = \int\limits_{1}^{2} x^2 \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^{2+1}}{2+1}\right]_{1}^{2} = \left[\frac{x^3}{3}\right]_{1}^{2}$
Substitute the upper limit $x=2$:
$\frac{2^3}{3} = \frac{8}{3}$
Substitute the lower limit $x=1$:
$\frac{1^3}{3} = \frac{1}{3}$
Evaluate the definite integral:
$A = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}$
Final Answer:
The area under the curve $y = x^2$ between $x = 1$ and $x = 2$ is $\frac{7}{3}$ square units.
(ii)
Given:
The bounding curves and lines are:
1. Curve: $y = x^4$
2. Line: $x = 1$
3. Line: $x = 5$
4. The x-axis ($y = 0$)
To Find:
The area of the region bounded by the given curve and lines.
Solution:
The given curve is $y = x^4$. The lines are $x=1$ and $x=5$, and the x-axis $y=0$.
In the interval $[1, 5]$, the function $y = x^4$ is non-negative ($x^4 \ge 0$).
The area of the region bounded by the curve $y = x^4$, the lines $x = 1$, $x = 5$, and the x-axis is given by the definite integral of $y = x^4$ from $x=1$ to $x=5$.
Area $A = \int\limits_{1}^{5} x^4 \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^{4+1}}{4+1}\right]_{1}^{5} = \left[\frac{x^5}{5}\right]_{1}^{5}$
Substitute the upper limit $x=5$:
$\frac{5^5}{5} = 5^{5-1} = 5^4 = 625$
Substitute the lower limit $x=1$:
$\frac{1^5}{5} = \frac{1}{5}$
Evaluate the definite integral:
$A = 625 - \frac{1}{5} = \frac{3125}{5} - \frac{1}{5} = \frac{3124}{5}$
Final Answer:
The area under the curve $y = x^4$ between $x = 1$ and $x = 5$ is $\frac{3124}{5}$ square units.
Question 2. Find the area between the curves y = x and y = x2 .
Answer:
Given:
The bounding curves are $y = x$ and $y = x^2$.
To Find:
The area of the region bounded by the given curves.
Solution:
The given curves are $y = x$ and $y = x^2$.
To find the points of intersection, we set the equations equal to each other:
$x^2 = x$
$x^2 - x = 0$
$x(x - 1) = 0$
This gives the x-coordinates of the intersection points: $x = 0$ and $x = 1$.
Find the corresponding y-values using either equation (e.g., $y=x$):
If $x = 0$, $y = 0$. Intersection point is $(0, 0)$.
If $x = 1$, $y = 1$. Intersection point is $(1, 1)$.
The region bounded by the two curves is between $x = 0$ and $x = 1$.
In the interval $(0, 1)$, let's determine which curve is above the other. Consider a test value, say $x = 0.5$.
For $y = x$, $y = 0.5$.
For $y = x^2$, $y = (0.5)^2 = 0.25$.
Since $0.5 > 0.25$, the line $y = x$ is above the parabola $y = x^2$ in the interval $(0, 1)$.
The area of the bounded region is given by the integral of the difference between the upper curve ($y = x$) and the lower curve ($y = x^2$) with respect to $x$ from $x = 0$ to $x = 1$.
Area $A = \int\limits_{0}^{1} (x - x^2) \$ dx$
Now, we evaluate the integral:
$A = \left[\frac{x^{1+1}}{1+1} - \frac{x^{2+1}}{2+1}\right]_{0}^{1}$
$A = \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1}$
Substitute the upper limit $x=1$:
$\left(\frac{1^2}{2} - \frac{1^3}{3}\right) = \left(\frac{1}{2} - \frac{1}{3}\right) = \frac{3}{6} - \frac{2}{6} = \frac{1}{6}$
Substitute the lower limit $x=0$:
$\left(\frac{0^2}{2} - \frac{0^3}{3}\right) = (0 - 0) = 0$
Evaluate the definite integral:
$A = \frac{1}{6} - 0 = \frac{1}{6}$
Final Answer:
The area between the curves $y = x$ and $y = x^2$ is $\frac{1}{6}$ square units.
Question 3. Find the area of the region lying in the first quadrant and bounded by y = 4x2 , x = 0, y = 1 and y = 4.
Answer:
Given:
The region is in the first quadrant and is bounded by:
1. Curve: $y = 4x^2$
2. Line: $x = 0$ (y-axis)
3. Line: $y = 1$
4. Line: $y = 4$
To Find:
The area of the specified region in the first quadrant.
Solution:
The given curve is $y = 4x^2$. For the first quadrant ($x \ge 0$), this can be written as $x^2 = \frac{y}{4}$, which implies $x = \sqrt{\frac{y}{4}} = \frac{\sqrt{y}}{2}$. This is the right half of a parabola opening upwards, with vertex at $(0,0)$.
The region is bounded on the left by the y-axis ($x=0$) and on the right by the parabola $x = \frac{\sqrt{y}}{2}$. The region is also bounded below by the line $y=1$ and above by the line $y=4$.
Since the boundaries are defined by constant values of y and the curve is given as $x$ in terms of $y$, it is convenient to integrate with respect to $y$. The integration will be performed from $y=1$ to $y=4$.
The area of the region is given by the integral of the function $x = \frac{\sqrt{y}}{2}$ from $y=1$ to $y=4$ with respect to $y$.
Area $A = \int\limits_{1}^{4} x \$ dy$
$A = \int\limits_{1}^{4} \frac{\sqrt{y}}{2} \$ dy$
$A = \frac{1}{2} \int\limits_{1}^{4} y^{1/2} \$ dy$
Now, we evaluate the integral:
The antiderivative of $y^{1/2}$ is $\frac{y^{1/2 + 1}}{1/2 + 1} = \frac{y^{3/2}}{3/2} = \frac{2}{3}y^{3/2}$.
$A = \frac{1}{2} \left[\frac{2}{3}y^{3/2}\right]_{1}^{4}$
$A = \frac{1}{3} \left[y^{3/2}\right]_{1}^{4}$
Substitute the upper limit $y=4$:
$(4)^{3/2} = (\sqrt{4})^3 = 2^3 = 8$
Substitute the lower limit $y=1$:
$(1)^{3/2} = (\sqrt{1})^3 = 1^3 = 1$
Evaluate the definite integral:
$A = \frac{1}{3} (8 - 1)$
$A = \frac{1}{3} (7)$
$A = \frac{7}{3}$
Final Answer:
The area of the region lying in the first quadrant and bounded by $y = 4x^2$, $x = 0$, $y = 1$, and $y = 4$ is $\frac{7}{3}$ square units.
Question 4. Sketch the graph of y = |x + 3| and evaluate $\int\limits_{−6}^0 |x + 3| \;dx$.
Answer:
Given:
The curve is $y = |x + 3|$.
The integral is $\int\limits_{-6}^0 |x + 3| \;dx$.
To Find:
Sketch the graph of $y = |x + 3|$ and evaluate the definite integral.
Solution:
The function $y = |x + 3|$ is an absolute value function. The vertex of the graph occurs where the expression inside the absolute value is zero, i.e., $x + 3 = 0$, which gives $x = -3$. When $x = -3$, $y = |-3 + 3| = 0$. So, the vertex is at $(-3, 0)$.
The function can be defined piecewise as:
$y = |x + 3| = \begin{cases} x + 3 & , & x + 3 \geq 0 \implies x \geq -3 \\ -(x + 3) = -x - 3 & , & x + 3 < 0 \implies x < -3 \end{cases}$
The graph of $y = |x + 3|$ is a V-shaped graph with its vertex at $(-3, 0)$. It opens upwards.
To sketch the graph, we can plot the vertex and a few points on either side:
Vertex: $(-3, 0)$
For $x \ge -3$: e.g., $x = -2 \implies y = |-2 + 3| = 1$, point $(-2, 1)$; $x = 0 \implies y = |0 + 3| = 3$, point $(0, 3)$.
For $x < -3$: e.g., $x = -4 \implies y = |-4 + 3| = |-1| = 1$, point $(-4, 1)$; $x = -6 \implies y = |-6 + 3| = |-3| = 3$, point $(-6, 3)$.
The graph consists of two linear pieces joined at $(-3, 0)$. The piece for $x \ge -3$ is the line $y = x + 3$ (slope 1). The piece for $x < -3$ is the line $y = -x - 3$ (slope -1).
We need to evaluate the definite integral $\int\limits_{-6}^0 |x + 3| \$ dx$.
The interval of integration is $[-6, 0]$. The point $x = -3$ where $|x+3|$ changes definition is within this interval.
We split the integral at $x = -3$:
$\int\limits_{-6}^0 |x + 3| \$ dx = \int\limits_{-6}^{-3} |x + 3| \$ dx + \int\limits_{-3}^{0} |x + 3| \$ dx$
For the interval $[-6, -3)$, $x < -3$, so $|x + 3| = -(x + 3) = -x - 3$.
For the interval $[-3, 0]$, $x \ge -3$, so $|x + 3| = x + 3$.
So, the integral becomes:
$\int\limits_{-6}^0 |x + 3| \$ dx = \int\limits_{-6}^{-3} (-x - 3) \$ dx + \int\limits_{-3}^{0} (x + 3) \$ dx$
Evaluate the first integral:
$\int\limits_{-6}^{-3} (-x - 3) \$ dx = \left[-\frac{x^2}{2} - 3x\right]_{-6}^{-3}$
$= \left(-\frac{(-3)^2}{2} - 3(-3)\right) - \left(-\frac{(-6)^2}{2} - 3(-6)\right)$
$= \left(-\frac{9}{2} + 9\right) - \left(-\frac{36}{2} + 18\right)$
$= \left(-\frac{9}{2} + \frac{18}{2}\right) - (-18 + 18)$
$= \frac{9}{2} - 0 = \frac{9}{2}$
Evaluate the second integral:
$\int\limits_{-3}^{0} (x + 3) \$ dx = \left[\frac{x^2}{2} + 3x\right]_{-3}^{0}$
$= \left(\frac{0^2}{2} + 3(0)\right) - \left(\frac{(-3)^2}{2} + 3(-3)\right)$
$= (0 + 0) - \left(\frac{9}{2} - 9\right)$
$= 0 - \left(\frac{9}{2} - \frac{18}{2}\right)$
$= 0 - \left(-\frac{9}{2}\right) = \frac{9}{2}$
The total value of the integral is the sum of the two results:
$\int\limits_{-6}^0 |x + 3| \$ dx = \frac{9}{2} + \frac{9}{2} = \frac{18}{2} = 9$
Geometrically, this integral represents the area of the region bounded by the graph of $y = |x + 3|$, the x-axis, and the lines $x = -6$ and $x = 0$. This region is composed of two triangles:
Triangle 1: Vertices at $(-6, 0)$, $(-3, 0)$, and $(-6, 3)$. Base length on the x-axis is $|-3 - (-6)| = 3$. Height is the y-value at $x=-6$, which is $|-6+3|=3$. Area $= \frac{1}{2} \times 3 \times 3 = \frac{9}{2}$.
Triangle 2: Vertices at $(-3, 0)$, $(0, 0)$, and $(0, 3)$. Base length on the x-axis is $|0 - (-3)| = 3$. Height is the y-value at $x=0$, which is $|0+3|=3$. Area $= \frac{1}{2} \times 3 \times 3 = \frac{9}{2}$.
Total Area $= \frac{9}{2} + \frac{9}{2} = 9$. This matches the integral result.
Final Answer:
The value of the integral $\int\limits_{-6}^0 |x + 3| \$ dx$ is 9.
Question 5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Answer:
Given:
The curve is $y = \sin x$.
The interval is from $x = 0$ to $x = 2\pi$.
To Find:
The area bounded by the curve, the x-axis, and the lines $x = 0$ and $x = 2\pi$.
Solution:
The area bounded by a curve $y = f(x)$ and the x-axis from $x=a$ to $x=b$ is given by $\int\limits_{a}^{b} |f(x)| \$ dx$.
In this case, we need to find the area $\int\limits_{0}^{2\pi} |\sin x| \$ dx$.
We need to determine the intervals where $\sin x$ is positive and where it is negative in the interval $[0, 2\pi]$.
$\sin x = 0$ at $x = 0$, $x = \pi$, and $x = 2\pi$ in the interval $[0, 2\pi]$.
The intervals are $[0, \pi]$ and $[\pi, 2\pi]$.
In $[0, \pi]$, $\sin x \ge 0$.
In $[\pi, 2\pi]$, $\sin x \le 0$.
So, the total area is the sum of the absolute values of the integrals over these intervals:
$A = \int\limits_{0}^{2\pi} |\sin x| \$ dx = \int\limits_{0}^{\pi} |\sin x| \$ dx + \int\limits_{\pi}^{2\pi} |\sin x| \$ dx$
$A = \int\limits_{0}^{\pi} \sin x \$ dx + \int\limits_{\pi}^{2\pi} (-\sin x) \$ dx$
Now, evaluate each integral:
$\int \sin x \$ dx = -\cos x$
$\int\limits_{0}^{\pi} \sin x \$ dx = [-\cos x]_{0}^{\pi} = (-\cos \pi) - (-\cos 0) = (-(-1)) - (-1) = 1 + 1 = 2$
$\int\limits_{\pi}^{2\pi} (-\sin x) \$ dx = [\cos x]_{\pi}^{2\pi} = \cos(2\pi) - \cos(\pi) = 1 - (-1) = 1 + 1 = 2$
Add the values of the integrals to find the total area:
$A = 2 + 2 = 4$
Final Answer:
The area bounded by the curve $y = \sin x$ between $x = 0$ and $x = 2\pi$ is 4 square units.
Question 6. Find the area enclosed between the parabola y2 = 4ax and the line y = mx.
Answer:
Given:
Equation of the parabola: $y^2 = 4ax$
Equation of the line: $y = mx$
To Find:
The area enclosed between the parabola and the line.
Solution:
First, we find the points of intersection of the parabola and the line.
Substitute $y = mx$ into the equation of the parabola:
$(mx)^2 = 4ax$
$m^2x^2 = 4ax$
$m^2x^2 - 4ax = 0$
$x(m^2x - 4a) = 0$
This gives two possible values for $x$:
$x = 0$
or
$m^2x - 4a = 0 \implies m^2x = 4a \implies x = \frac{4a}{m^2}$ (assuming $m \neq 0$)
For $x = 0$, $y = m(0) = 0$. One intersection point is $(0, 0)$.
For $x = \frac{4a}{m^2}$, $y = m\left(\frac{4a}{m^2}\right) = \frac{4a}{m}$. The other intersection point is $\left(\frac{4a}{m^2}, \frac{4a}{m}\right)$.
The enclosed area is bounded by the line segment connecting $(0,0)$ and $\left(\frac{4a}{m^2}, \frac{4a}{m}\right)$ and the corresponding arc of the parabola.
To find the area, we can integrate with respect to $y$. We need to express $x$ in terms of $y$ for both curves:
From the parabola $y^2 = 4ax$, we have $x = \frac{y^2}{4a}$.
From the line $y = mx$, we have $x = \frac{y}{m}$.
The y-coordinates of the intersection points are $y_1 = 0$ and $y_2 = \frac{4a}{m}$.
In the region between the intersection points (for $y$ between $0$ and $\frac{4a}{m}$), the line $x = \frac{y}{m}$ is to the right of the parabola $x = \frac{y^2}{4a}$. That is, $\frac{y}{m} \geq \frac{y^2}{4a}$.
The area $A$ is given by the integral of the difference between the rightmost curve and the leftmost curve with respect to $y$, from the lower y-limit to the upper y-limit.
$A = \int_{y_1}^{y_2} (x_{line} - x_{parabola}) dy$
$A = \int_{0}^{\frac{4a}{m}} \left( \frac{y}{m} - \frac{y^2}{4a} \right) dy$
Note: The limits are $0$ to $\frac{4a}{m}$. If $\frac{4a}{m}$ is negative (i.e., $a$ and $m$ have opposite signs, assuming $a>0$), the integration direction ensures a positive area result, or we can take the absolute value of the integral $\left| \int_{0}^{\frac{4a}{m}} \left( \frac{y}{m} - \frac{y^2}{4a} \right) dy \right|$. Let's evaluate the indefinite integral first.
$\int \left( \frac{y}{m} - \frac{y^2}{4a} \right) dy = \frac{1}{m} \int y \, dy - \frac{1}{4a} \int y^2 \, dy$
$= \frac{1}{m} \frac{y^2}{2} - \frac{1}{4a} \frac{y^3}{3} + C$
$= \frac{y^2}{2m} - \frac{y^3}{12a} + C$
Now, evaluate the definite integral with the limits $0$ and $\frac{4a}{m}$.
$A = \left[ \frac{y^2}{2m} - \frac{y^3}{12a} \right]_{0}^{\frac{4a}{m}}$
$A = \left( \frac{1}{2m} \left(\frac{4a}{m}\right)^2 - \frac{1}{12a} \left(\frac{4a}{m}\right)^3 \right) - \left( \frac{0^2}{2m} - \frac{0^3}{12a} \right)$
$A = \left( \frac{1}{2m} \cdot \frac{16a^2}{m^2} - \frac{1}{12a} \cdot \frac{64a^3}{m^3} \right) - 0$
$A = \frac{16a^2}{2m^3} - \frac{64a^3}{12am^3}$
$A = \frac{8a^2}{m^3} - \frac{\cancel{64}^{16}a^{\cancel{3}^{2}}}{\cancel{12}^{3}\cancel{a}m^3}$
$A = \frac{8a^2}{m^3} - \frac{16a^2}{3m^3}$
$A = \frac{3 \cdot 8a^2 - 16a^2}{3m^3}$
$A = \frac{24a^2 - 16a^2}{3m^3}$
$A = \frac{8a^2}{3m^3}$
Since area is a positive quantity, the result should be interpreted as the absolute value if $m$ is negative. However, the standard formula is given as $\frac{8a^2}{3m^3}$, assuming $a>0$ and considering the signed area or implying $m>0$. We provide the standard formula as the result.
The area enclosed between the parabola $y^2 = 4ax$ and the line $y = mx$ is $\frac{8a^2}{3m^3}$ square units.
Question 7. Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12.
Answer:
Given:
Equation of the parabola: $4y = 3x^2 \implies y = \frac{3}{4}x^2$
Equation of the line: $2y = 3x + 12 \implies y = \frac{3}{2}x + 6$
To Find:
The area enclosed by the parabola and the line.
Solution:
First, we find the points of intersection of the parabola and the line by setting their y-values equal:
$\frac{3}{4}x^2 = \frac{3}{2}x + 6$
Multiply the entire equation by 4 to eliminate denominators:
$3x^2 = 6x + 24$
Rearrange the terms to form a quadratic equation:
$3x^2 - 6x - 24 = 0$
Divide by 3:
$x^2 - 2x - 8 = 0$
Factor the quadratic equation:
$(x - 4)(x + 2) = 0$
The x-coordinates of the intersection points are $x = 4$ and $x = -2$.
We can find the corresponding y-coordinates using the equation of the line $y = \frac{3}{2}x + 6$:
For $x = 4$: $y = \frac{3}{2}(4) + 6 = 6 + 6 = 12$. Intersection point: $(4, 12)$.
For $x = -2$: $y = \frac{3}{2}(-2) + 6 = -3 + 6 = 3$. Intersection point: $(-2, 3)$.
The enclosed area is bounded by the line from $x = -2$ to $x = 4$ and the parabola from $x = -2$ to $x = 4$.
To determine which curve is above the other in the interval $[-2, 4]$, we can test a value, for example, $x = 0$:
Line: $y = \frac{3}{2}(0) + 6 = 6$
Parabola: $y = \frac{3}{4}(0)^2 = 0$
Since $6 > 0$, the line is above the parabola in the interval $[-2, 4]$.
The area $A$ enclosed by the two curves is given by the definite integral of the difference between the upper curve ($y_{line}$) and the lower curve ($y_{parabola}$) with respect to $x$, from $x = -2$ to $x = 4$:
$A = \int_{-2}^{4} (y_{line} - y_{parabola}) dx$
$A = \int_{-2}^{4} \left( \left(\frac{3}{2}x + 6\right) - \left(\frac{3}{4}x^2\right) \right) dx$
$A = \int_{-2}^{4} \left( \frac{3}{2}x + 6 - \frac{3}{4}x^2 \right) dx$
Now, we evaluate the integral:
$A = \left[ \frac{3}{2}\frac{x^2}{2} + 6x - \frac{3}{4}\frac{x^3}{3} \right]_{-2}^{4}$
$A = \left[ \frac{3}{4}x^2 + 6x - \frac{1}{4}x^3 \right]_{-2}^{4}$
Evaluate the expression at the upper limit ($x=4$):
$\left( \frac{3}{4}(4)^2 + 6(4) - \frac{1}{4}(4)^3 \right) = \left( \frac{3}{4}(16) + 24 - \frac{1}{4}(64) \right) = (12 + 24 - 16) = 20$
Evaluate the expression at the lower limit ($x=-2$):
$\left( \frac{3}{4}(-2)^2 + 6(-2) - \frac{1}{4}(-2)^3 \right) = \left( \frac{3}{4}(4) - 12 - \frac{1}{4}(-8) \right) = (3 - 12 + 2) = -7$
Subtract the value at the lower limit from the value at the upper limit:
$A = 20 - (-7) = 20 + 7 = 27$
The area enclosed by the parabola $4y = 3x^2$ and the line $2y = 3x + 12$ is $27$ square units.
Question 8. Find the area of the smaller region bounded by the ellipse $\frac{x^2}{9} + \frac{y^2}{4} = 1$ and the line $\frac{x}{3} + \frac{y}{2} = 1$.
Answer:
Given:
Equation of the ellipse: $\frac{x^2}{9} + \frac{y^2}{4} = 1$
Equation of the line: $\frac{x}{3} + \frac{y}{2} = 1$
To Find:
The area of the smaller region bounded by the ellipse and the line.
Solution:
The given equation of the ellipse is $\frac{x^2}{9} + \frac{y^2}{4} = 1$. This is in the standard form $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, where $a^2 = 9 \implies a=3$ and $b^2 = 4 \implies b=2$. The ellipse intersects the x-axis at $(\pm 3, 0)$ and the y-axis at $(0, \pm 2)$.
The given equation of the line is $\frac{x}{3} + \frac{y}{2} = 1$. This is in the intercept form $\frac{x}{\text{x-intercept}} + \frac{y}{\text{y-intercept}} = 1$. The line intersects the x-axis at $(3, 0)$ and the y-axis at $(0, 2)$.
We observe that the points of intersection of the line with the coordinate axes, $(3, 0)$ and $(0, 2)$, are also the points where the ellipse intersects the positive x-axis and positive y-axis, respectively.
To confirm these are intersection points, we can substitute $(3,0)$ into the ellipse equation: $\frac{3^2}{9} + \frac{0^2}{4} = \frac{9}{9} + 0 = 1$, which is true. Substitute $(0,2)$ into the ellipse equation: $\frac{0^2}{9} + \frac{2^2}{4} = 0 + \frac{4}{4} = 1$, which is true.
The line segment connecting $(3, 0)$ and $(0, 2)$ forms a chord of the ellipse. The smaller region bounded by the ellipse and the line is the area of the segment cut off by this chord in the first quadrant.
This area can be found by subtracting the area of the triangle formed by the line and the coordinate axes in the first quadrant from the area of the part of the ellipse in the first quadrant.
Area of the part of the ellipse in the first quadrant:
From the ellipse equation $\frac{x^2}{9} + \frac{y^2}{4} = 1$, we can express $y$ in terms of $x$ for the upper half ($y \ge 0$):
$\frac{y^2}{4} = 1 - \frac{x^2}{9} = \frac{9 - x^2}{9}$
$y^2 = \frac{4}{9}(9 - x^2)$
$y = \frac{2}{3}\sqrt{9 - x^2}$
The area under the ellipse in the first quadrant (from $x=0$ to $x=3$) is given by the integral:
$A_{ellipse, Q1} = \int_{0}^{3} \frac{2}{3}\sqrt{9 - x^2} \, dx$
$= \frac{2}{3} \int_{0}^{3} \sqrt{3^2 - x^2} \, dx$
Using the standard integral formula $\int \sqrt{a^2 - x^2} \, dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$, with $a=3$:
$A_{ellipse, Q1} = \frac{2}{3} \left[ \frac{x}{2}\sqrt{9 - x^2} + \frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right) \right]_{0}^{3}$
$= \frac{2}{3} \left[ \left( \frac{3}{2}\sqrt{9 - 3^2} + \frac{9}{2}\sin^{-1}\left(\frac{3}{3}\right) \right) - \left( \frac{0}{2}\sqrt{9 - 0^2} + \frac{9}{2}\sin^{-1}\left(\frac{0}{3}\right) \right) \right]$
$= \frac{2}{3} \left[ \left( \frac{3}{2}\sqrt{0} + \frac{9}{2}\sin^{-1}(1) \right) - \left( 0 + \frac{9}{2}\sin^{-1}(0) \right) \right]$
$= \frac{2}{3} \left[ \left( 0 + \frac{9}{2} \cdot \frac{\pi}{2} \right) - \left( 0 + 0 \right) \right]$
$= \frac{2}{3} \left( \frac{9\pi}{4} \right) = \frac{\cancel{2}}{\cancel{3}} \cdot \frac{\cancel{9}^{3}\pi}{\cancel{4}^{2}} = \frac{3\pi}{2}$
Area of the triangle formed by the line and the axes:
The line $\frac{x}{3} + \frac{y}{2} = 1$ forms a triangle in the first quadrant with vertices at $(0,0)$, $(3,0)$, and $(0,2)$. This is a right-angled triangle with base 3 (along the x-axis) and height 2 (along the y-axis).
$A_{triangle} = \frac{1}{2} \times \text{base} \times \text{height}$
$A_{triangle} = \frac{1}{2} \times 3 \times 2 = 3$
Area of the smaller region:
The area of the smaller region is the area of the ellipse in the first quadrant minus the area of the triangle.
$A_{region} = A_{ellipse, Q1} - A_{triangle}$
$A_{region} = \frac{3\pi}{2} - 3$
The area of the smaller region bounded by the ellipse $\frac{x^2}{9} + \frac{y^2}{4} = 1$ and the line $\frac{x}{3} + \frac{y}{2} = 1$ is $\left(\frac{3\pi}{2} - 3\right)$ square units.
Question 9. Find the area of the smaller region bounded by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ and the $\frac{x}{a} + \frac{y}{b} = 1$.
Answer:
Given:
Equation of the ellipse: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
Equation of the line: $\frac{x}{a} + \frac{y}{b} = 1$
To Find:
The area of the smaller region bounded by the ellipse and the line.
Solution:
The equation of the ellipse is $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. This ellipse is centered at the origin and intersects the positive x-axis at $(a, 0)$ and the positive y-axis at $(0, b)$.
The equation of the line is $\frac{x}{a} + \frac{y}{b} = 1$. This line is in intercept form and passes through the points $(a, 0)$ and $(0, b)$.
The points $(a, 0)$ and $(0, b)$ lie on both the ellipse and the line, as substituting these coordinates into the ellipse equation gives $\frac{a^2}{a^2} + \frac{0^2}{b^2} = 1 + 0 = 1$ and $\frac{0^2}{a^2} + \frac{b^2}{b^2} = 0 + 1 = 1$, respectively.
The smaller region bounded by the ellipse and the line is the area of the segment of the ellipse cut off by the line segment connecting $(a, 0)$ and $(0, b)$. This region is located in the first quadrant.
The area of this region can be calculated by subtracting the area of the triangle formed by the line $\frac{x}{a} + \frac{y}{b} = 1$ and the coordinate axes in the first quadrant from the area of the part of the ellipse in the first quadrant.
Area of the part of the ellipse in the first quadrant:
From the ellipse equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, we solve for $y$ in the first quadrant ($y \ge 0$):
$\frac{y^2}{b^2} = 1 - \frac{x^2}{a^2} = \frac{a^2 - x^2}{a^2}$
$y^2 = \frac{b^2}{a^2}(a^2 - x^2)$
$y = \frac{b}{a}\sqrt{a^2 - x^2}$
The area under the ellipse in the first quadrant (from $x=0$ to $x=a$) is given by the integral:
$A_{\text{ellipse, Q1}} = \int_{0}^{a} \frac{b}{a}\sqrt{a^2 - x^2} \, dx$
$= \frac{b}{a} \int_{0}^{a} \sqrt{a^2 - x^2} \, dx$
Using the standard integral formula $\int \sqrt{a^2 - x^2} \, dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)$, we get:
$A_{\text{ellipse, Q1}} = \frac{b}{a} \left[ \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right) \right]_{0}^{a}$
Evaluating the definite integral:
$A_{\text{ellipse, Q1}} = \frac{b}{a} \left[ \left( \frac{a}{2}\sqrt{a^2 - a^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{a}{a}\right) \right) - \left( \frac{0}{2}\sqrt{a^2 - 0^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{0}{a}\right) \right) \right]$
$= \frac{b}{a} \left[ \left( 0 + \frac{a^2}{2}\sin^{-1}(1) \right) - \left( 0 + \frac{a^2}{2}\sin^{-1}(0) \right) \right]$
$= \frac{b}{a} \left[ \left( \frac{a^2}{2} \cdot \frac{\pi}{2} \right) - 0 \right]$
$= \frac{b}{a} \cdot \frac{\pi a^2}{4} = \frac{\pi ab}{4}$
Area of the triangle formed by the line and the axes:
The line $\frac{x}{a} + \frac{y}{b} = 1$ forms a right-angled triangle with the positive x-axis and positive y-axis. The vertices of the triangle are $(0,0)$, $(a,0)$, and $(0,b)$.
The base of the triangle is $a$ (along the x-axis) and the height is $b$ (along the y-axis).
$A_{\text{triangle}} = \frac{1}{2} \times \text{base} \times \text{height}$
$A_{\text{triangle}} = \frac{1}{2} \times a \times b = \frac{ab}{2}$
Area of the smaller region:
The area of the smaller region is the area of the ellipse in the first quadrant minus the area of the triangle.
$A_{\text{region}} = A_{\text{ellipse, Q1}} - A_{\text{triangle}}$
$A_{\text{region}} = \frac{\pi ab}{4} - \frac{ab}{2}$
$A_{\text{region}} = ab \left( \frac{\pi}{4} - \frac{1}{2} \right)$
$A_{\text{region}} = ab \left( \frac{\pi - 2}{4} \right)$
$A_{\text{region}} = \frac{ab}{4}(\pi - 2)$
The area of the smaller region bounded by the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ and the line $\frac{x}{a} + \frac{y}{b} = 1$ is $\frac{ab}{4}(\pi - 2)$ square units.
Question 10. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
Answer:
Given:
Equation of the parabola: $y = x^2$
Equation of the line: $y = x + 2$}
Equation of the x-axis: $y = 0$
To Find:
The area of the region enclosed by the parabola, the line, and the x-axis.
Solution:
First, find the intersection points of the curves:
1. Intersection of the line $y = x + 2$ and the x-axis $y = 0$:
$0 = x + 2 \implies x = -2$. Intersection point: $(-2, 0)$.
2. Intersection of the parabola $y = x^2$ and the x-axis $y = 0$:
$0 = x^2 \implies x = 0$. Intersection point: $(0, 0)$.
3. Intersection of the line $y = x + 2$ and the parabola $y = x^2$:
$x^2 = x + 2$
$x^2 - x - 2 = 0$
$(x - 2)(x + 1) = 0$
This gives $x = 2$ or $x = -1$.
For $x = 2$, $y = 2 + 2 = 4$. Intersection point: $(2, 4)$.
For $x = -1$, $y = -1 + 2 = 1$. Intersection point: $(-1, 1)$.
The points of intersection are $(-2, 0)$, $(0, 0)$, $(-1, 1)$, and $(2, 4)$.
Let's visualize the region enclosed by all three curves. The line $y=x+2$ intersects the x-axis at $x=-2$. The parabola $y=x^2$ intersects the x-axis at $x=0$. The line and parabola intersect at $x=-1$ and $x=2$. The region enclosed by all three is bounded by the line from $x=-2$ to $x=-1$, by the parabola from $x=-1$ to $x=0$, and by the x-axis from $x=-2$ to $x=0$. The vertices of this region are $(-2,0)$, $(-1,1)$, and $(0,0)$.
We can find the area by integrating with respect to $x$, splitting the integral at $x=-1$.
From $x=-2$ to $x=-1$, the upper boundary is the line $y = x + 2$ and the lower boundary is the x-axis $y = 0$. The area of this part is $\int_{-2}^{-1} (x+2 - 0) dx = \int_{-2}^{-1} (x+2) dx$.
From $x=-1$ to $x=0$, the upper boundary is the parabola $y = x^2$ and the lower boundary is the x-axis $y = 0$. The area of this part is $\int_{-1}^{0} (x^2 - 0) dx = \int_{-1}^{0} x^2 dx$.
The total area is the sum of these two integrals:
$A = \int_{-2}^{-1} (x+2) dx + \int_{-1}^{0} x^2 dx$
Evaluate the first integral:
$\int_{-2}^{-1} (x+2) dx = \left[ \frac{x^2}{2} + 2x \right]_{-2}^{-1}$
$= \left( \frac{(-1)^2}{2} + 2(-1) \right) - \left( \frac{(-2)^2}{2} + 2(-2) \right)$
$= \left( \frac{1}{2} - 2 \right) - \left( \frac{4}{2} - 4 \right)$
$= \left( -\frac{3}{2} \right) - (2 - 4)$
$= -\frac{3}{2} - (-2) = -\frac{3}{2} + 2 = \frac{-3 + 4}{2} = \frac{1}{2}$
Evaluate the second integral:
$\int_{-1}^{0} x^2 dx = \left[ \frac{x^3}{3} \right]_{-1}^{0}$
$= \frac{0^3}{3} - \frac{(-1)^3}{3}$
$= 0 - \left(-\frac{1}{3}\right) = \frac{1}{3}$
Calculate the total area:
$A = \frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6}$
The area of the region enclosed by the parabola $x^2 = y$, the line $y = x + 2$ and the x-axis is $\frac{5}{6}$ square units.
Question 11. Using the method of integration find the area bounded by the curve |x| + |y| = 1.
[Hint: The required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 1].
Answer:
Given:
Equation of the curve: $|x| + |y| = 1$
To Find:
The area bounded by the curve $|x| + |y| = 1$ using the method of integration.
Solution:
The equation $|x| + |y| = 1$ represents four line segments in the four different quadrants:
1. In the first quadrant ($x \ge 0, y \ge 0$): $x + y = 1 \implies y = 1 - x$
2. In the second quadrant ($x \le 0, y \ge 0$): $-x + y = 1 \implies y = 1 + x$
3. In the third quadrant ($x \le 0, y \le 0$): $-x - y = 1 \implies y = -1 - x$
4. In the fourth quadrant ($x \ge 0, y \le 0$): $x - y = 1 \implies y = x - 1$
These lines form a square with vertices at $(1, 0)$, $(0, 1)$, $(-1, 0)$, and $(0, -1)$.
The region is symmetric with respect to the x-axis, the y-axis, and the origin. Therefore, we can calculate the area of the region in the first quadrant and multiply it by 4 to get the total area.
In the first quadrant, the region is bounded by the line $y = 1 - x$, the x-axis ($y=0$), and the y-axis ($x=0$). This region is a triangle with vertices $(0,0)$, $(1,0)$, and $(0,1)$.
The area in the first quadrant ($A_{Q1}$) can be found by integrating the function $y = 1 - x$ with respect to $x$ from $x=0$ to $x=1$.
$A_{Q1} = \int_{0}^{1} (1 - x) \, dx$
Evaluate the integral:
$A_{Q1} = \left[ x - \frac{x^2}{2} \right]_{0}^{1}$
$A_{Q1} = \left( 1 - \frac{1^2}{2} \right) - \left( 0 - \frac{0^2}{2} \right)$
$A_{Q1} = \left( 1 - \frac{1}{2} \right) - 0$
$A_{Q1} = \frac{1}{2}$
The total area ($A_{total}$) is 4 times the area in the first quadrant:
$A_{total} = 4 \times A_{Q1}$
$A_{total} = 4 \times \frac{1}{2}$
$A_{total} = 2$
The area bounded by the curve $|x| + |y| = 1$ is $2$ square units.
Question 12. Find the area bounded by curves {(x, y) : y ≥ x2 and y = | x |}.
Answer:
Given:
The region defined by $y \geq x^2$ and $y = |x|$.
To Find:
The area of the region bounded by the curves $y = x^2$ and $y = |x|$.
Solution:
The region is bounded by the parabola $y = x^2$ and the curve $y = |x|$.
The curve $y = |x|$ consists of two lines:
$y = x$ for $x \ge 0$
$y = -x$ for $x < 0$
First, we find the points of intersection of the curves $y = x^2$ and $y = |x|$.
Case 1: $x \ge 0$. The intersection is between $y = x^2$ and $y = x$.
$x^2 = x$
$x^2 - x = 0$
$x(x - 1) = 0$
$x = 0$ or $x = 1$
If $x = 0$, $y = 0^2 = 0$. Point: $(0, 0)$.
If $x = 1$, $y = 1^2 = 1$. Point: $(1, 1)$.
Case 2: $x < 0$. The intersection is between $y = x^2$ and $y = -x$.
$x^2 = -x$
$x^2 + x = 0$
$x(x + 1) = 0$
$x = 0$ or $x = -1$
Since we are in the case $x < 0$, we take $x = -1$.
If $x = -1$, $y = (-1)^2 = 1$. Point: $(-1, 1)$.
The intersection points are $(-1, 1)$, $(0, 0)$, and $(1, 1)$.
The region $y \geq x^2$ is the area above the parabola $y = x^2$. The region $y = |x|$ is the graph of the absolute value function. The bounded region described by the question is the area enclosed between the curves $y = |x|$ and $y = x^2$ where $y_{|x|} \ge y_{x^2}$.
The region is symmetric about the y-axis. We can find the area of the region in the first quadrant (bounded by $y = x^2$ and $y = x$ from $x=0$ to $x=1$) and multiply it by 2.
In the first quadrant ($0 \le x \le 1$), for any $x$ in this interval (except $x=0, 1$), we have $x > x^2$. For example, at $x = 0.5$, $y_{|x|} = 0.5$ and $y_{x^2} = 0.25$. Thus, the line $y=x$ is above the parabola $y=x^2$ in the interval $(0, 1)$.
The area of the region in the first quadrant ($A_{Q1}$) is given by the integral of the upper curve minus the lower curve from $x=0$ to $x=1$:
$A_{Q1} = \int_{0}^{1} (x - x^2) \, dx$
Evaluate the integral:
$A_{Q1} = \left[ \frac{x^2}{2} - \frac{x^3}{3} \right]_{0}^{1}$
$A_{Q1} = \left( \frac{1^2}{2} - \frac{1^3}{3} \right) - \left( \frac{0^2}{2} - \frac{0^3}{3} \right)$
$A_{Q1} = \left( \frac{1}{2} - \frac{1}{3} \right) - 0$
$A_{Q1} = \frac{3 - 2}{6} = \frac{1}{6}$
The total area is twice the area in the first quadrant due to symmetry:
$A_{total} = 2 \times A_{Q1}$
$A_{total} = 2 \times \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$
The area bounded by the curves $y = x^2$ and $y = |x|$ is $\frac{1}{3}$ square units.
Question 13. Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Answer:
Given:
Vertices of the triangle ABC are A(2, 0), B(4, 5), and C(6, 3).
To Find:
The area of the triangle ABC using the method of integration.
Solution:
To find the area of the triangle using integration, we need to determine the equations of the lines forming the sides of the triangle: AB, BC, and AC.
1. Equation of line AB: Passes through A(2, 0) and B(4, 5).
Slope $m_{AB} = \frac{5 - 0}{4 - 2} = \frac{5}{2}$
Equation using point-slope form $y - y_1 = m(x - x_1)$: $y - 0 = \frac{5}{2}(x - 2)$
$y = \frac{5}{2}x - 5$
2. Equation of line BC: Passes through B(4, 5) and C(6, 3).
Slope $m_{BC} = \frac{3 - 5}{6 - 4} = \frac{-2}{2} = -1$
Equation: $y - 5 = -1(x - 4) \implies y - 5 = -x + 4$
$y = -x + 9$
3. Equation of line AC: Passes through A(2, 0) and C(6, 3).
Slope $m_{AC} = \frac{3 - 0}{6 - 2} = \frac{3}{4}$
Equation: $y - 0 = \frac{3}{4}(x - 2)$
$y = \frac{3}{4}x - \frac{3}{2}$
The area of the triangle can be found by integrating with respect to $x$. The triangle's base lies on the x-axis along AC, but the segments AB and BC form the upper boundary. The x-coordinates of the vertices are 2, 4, and 6.
We can divide the area into two parts:
Part 1: Bounded by AB, AC from $x=2$ to $x=4$. The upper boundary is AB, the lower boundary is AC.
Part 2: Bounded by BC, AC from $x=4$ to $x=6$. The upper boundary is BC, the lower boundary is AC.
Area = $\int_{2}^{4} (y_{AB} - y_{AC}) \, dx + \int_{4}^{6} (y_{BC} - y_{AC}) \, dx$
Area = $\int_{2}^{4} \left(\left(\frac{5}{2}x - 5\right) - \left(\frac{3}{4}x - \frac{3}{2}\right)\right) \, dx + \int_{4}^{6} \left(\left(-x + 9\right) - \left(\frac{3}{4}x - \frac{3}{2}\right)\right) \, dx$}
Simplify the integrands:
For the first integral: $\frac{5}{2}x - 5 - \frac{3}{4}x + \frac{3}{2} = \left(\frac{10}{4} - \frac{3}{4}\right)x + \left(-5 + \frac{3}{2}\right) = \frac{7}{4}x - \frac{7}{2}$
For the second integral: $-x + 9 - \frac{3}{4}x + \frac{3}{2} = \left(-1 - \frac{3}{4}\right)x + \left(9 + \frac{3}{2}\right) = -\frac{7}{4}x + \frac{18+3}{2} = -\frac{7}{4}x + \frac{21}{2}$
Area = $\int_{2}^{4} \left(\frac{7}{4}x - \frac{7}{2}\right) \, dx + \int_{4}^{6} \left(-\frac{7}{4}x + \frac{21}{2}\right) \, dx$
Evaluate the first integral:
$\int_{2}^{4} \left(\frac{7}{4}x - \frac{7}{2}\right) \, dx = \left[ \frac{7}{4}\frac{x^2}{2} - \frac{7}{2}x \right]_{2}^{4} = \left[ \frac{7}{8}x^2 - \frac{7}{2}x \right]_{2}^{4}$
$= \left(\frac{7}{8}(4)^2 - \frac{7}{2}(4)\right) - \left(\frac{7}{8}(2)^2 - \frac{7}{2}(2)\right)$
$= \left(\frac{7}{8}(16) - 14\right) - \left(\frac{7}{8}(4) - 7\right)$
$= (14 - 14) - \left(\frac{7}{2} - 7\right) = 0 - \left(-\frac{7}{2}\right) = \frac{7}{2}$
Evaluate the second integral:
$\int_{4}^{6} \left(-\frac{7}{4}x + \frac{21}{2}\right) \, dx = \left[ -\frac{7}{4}\frac{x^2}{2} + \frac{21}{2}x \right]_{4}^{6} = \left[ -\frac{7}{8}x^2 + \frac{21}{2}x \right]_{4}^{6}$
$= \left(-\frac{7}{8}(6)^2 + \frac{21}{2}(6)\right) - \left(-\frac{7}{8}(4)^2 + \frac{21}{2}(4)\right)$
$= \left(-\frac{7}{8}(36) + 63\right) - \left(-\frac{7}{8}(16) + 42\right)$
$= \left(-\frac{63}{2} + 63\right) - (-14 + 42)$
$= \left(\frac{-63 + 126}{2}\right) - 28 = \frac{63}{2} - 28 = \frac{63 - 56}{2} = \frac{7}{2}$
Total Area = Sum of the two integral results:
Area = $\frac{7}{2} + \frac{7}{2} = \frac{14}{2} = 7$
The area of the triangle ABC is $7$ square units.
Question 14. Using the method of integration find the area of the region bounded by lines:
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Answer:
Given:
The equations of the three lines are:
Line 1 (L1): $2x + y = 4 \implies y = 4 - 2x$
Line 2 (L2): $3x - 2y = 6 \implies 2y = 3x - 6 \implies y = \frac{3}{2}x - 3$
Line 3 (L3): $x - 3y + 5 = 0 \implies 3y = x + 5 \implies y = \frac{1}{3}x + \frac{5}{3}$
To Find:
The area of the region bounded by the three given lines using the method of integration.
Solution:
The region bounded by the three lines is a triangle. To find the area, we first need to determine the vertices of the triangle, which are the points of intersection of the lines.
1. Intersection of L1 and L2:
$4 - 2x = \frac{3}{2}x - 3$
$8 - 4x = 3x - 6$
$14 = 7x$
$x = 2$
Substitute $x=2$ into L1: $y = 4 - 2(2) = 0$. Vertex P is $(2, 0)$.
2. Intersection of L1 and L3:
$4 - 2x = \frac{1}{3}x + \frac{5}{3}$
$12 - 6x = x + 5$
$7 = 7x$
$x = 1$
Substitute $x=1$ into L1: $y = 4 - 2(1) = 2$. Vertex Q is $(1, 2)$.
3. Intersection of L2 and L3:
$\frac{3}{2}x - 3 = \frac{1}{3}x + \frac{5}{3}$
$9x - 18 = 2x + 10$
$7x = 28$
$x = 4$
Substitute $x=4$ into L2: $y = \frac{3}{2}(4) - 3 = 6 - 3 = 3$. Vertex R is $(4, 3)$.
The vertices of the triangle are Q(1, 2), P(2, 0), and R(4, 3). We can find the area of this triangle by integrating with respect to $x$. The x-coordinates of the vertices are 1, 2, and 4.
The area can be calculated as the area under the upper boundary curve(s) minus the area under the lower boundary curve(s), integrated over the range of x-values of the triangle's vertices (from 1 to 4).
By inspecting the graph or comparing y-values in the interval $[1, 4]$, the line L3 ($y = \frac{1}{3}x + \frac{5}{3}$) forms the upper boundary of the triangle (connecting Q and R).
The lower boundary is formed by the line segment QP (L1: $y = 4 - 2x$) from $x=1$ to $x=2$ and the line segment PR (L2: $y = \frac{3}{2}x - 3$) from $x=2$ to $x=4$.
Area = $\int_{1}^{4} y_{L3} \, dx - \left( \int_{1}^{2} y_{L1} \, dx + \int_{2}^{4} y_{L2} \, dx \right)$
Area = $\int_{1}^{4} \left(\frac{1}{3}x + \frac{5}{3}\right) \, dx - \left( \int_{1}^{2} (4 - 2x) \, dx + \int_{2}^{4} \left(\frac{3}{2}x - 3\right) \, dx \right)$
Evaluate the integrals:
$\int_{1}^{4} \left(\frac{1}{3}x + \frac{5}{3}\right) \, dx = \left[ \frac{x^2}{6} + \frac{5x}{3} \right]_{1}^{4} = \left(\frac{4^2}{6} + \frac{5(4)}{3}\right) - \left(\frac{1^2}{6} + \frac{5(1)}{3}\right)$
$= \left(\frac{16}{6} + \frac{20}{3}\right) - \left(\frac{1}{6} + \frac{5}{3}\right) = \left(\frac{8}{3} + \frac{20}{3}\right) - \left(\frac{1}{6} + \frac{10}{6}\right) = \frac{28}{3} - \frac{11}{6} = \frac{56 - 11}{6} = \frac{45}{6} = \frac{15}{2}$
$\int_{1}^{2} (4 - 2x) \, dx = \left[ 4x - x^2 \right]_{1}^{2} = (4(2) - 2^2) - (4(1) - 1^2) = (8 - 4) - (4 - 1) = 4 - 3 = 1$}
$\int_{2}^{4} \left(\frac{3}{2}x - 3\right) \, dx = \left[ \frac{3x^2}{4} - 3x \right]_{2}^{4} = \left(\frac{3(4)^2}{4} - 3(4)\right) - \left(\frac{3(2)^2}{4} - 3(2)\right)$
$= \left(\frac{3(16)}{4} - 12\right) - \left(\frac{3(4)}{4} - 6\right) = (12 - 12) - (3 - 6) = 0 - (-3) = 3$}
Now, substitute these values back into the area formula:
Area $= \frac{15}{2} - (1 + 3) = \frac{15}{2} - 4 = \frac{15}{2} - \frac{8}{2} = \frac{7}{2}$
The area of the triangle bounded by the given lines is $\frac{7}{2}$ square units.
Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Answer:
Given:
The region is defined by the inequalities $y^2 \leq 4x$ and $4x^2 + 4y^2 \leq 9$.
The first inequality $y^2 \leq 4x$ represents the region on or to the right of the parabola $y^2 = 4x$.
The second inequality $4x^2 + 4y^2 \leq 9$ can be rewritten as $x^2 + y^2 \leq \frac{9}{4}$. This represents the region on or inside the circle centered at the origin with radius $r = \sqrt{\frac{9}{4}} = \frac{3}{2}$.
To Find:
The area of the region that satisfies both inequalities.
Solution:
The region is bounded by the parabola $y^2 = 4x$ and the circle $x^2 + y^2 = \frac{9}{4}$. We need to find the area of the intersection of the region to the right of the parabola and the region inside the circle.
First, find the points of intersection of the parabola $y^2 = 4x$ and the circle $x^2 + y^2 = \frac{9}{4}$. Substitute $y^2 = 4x$ into the circle equation:
$x^2 + 4x = \frac{9}{4}$
Multiply by 4 to clear the denominator:
$4x^2 + 16x = 9$
$4x^2 + 16x - 9 = 0$
Solve the quadratic equation for $x$ using the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:
$x = \frac{-16 \pm \sqrt{16^2 - 4(4)(-9)}}{2(4)}$
$x = \frac{-16 \pm \sqrt{256 + 144}}{8}$
$x = \frac{-16 \pm \sqrt{400}}{8}$
$x = \frac{-16 \pm 20}{8}$
Two possible values for $x$ are $x_1 = \frac{-16 + 20}{8} = \frac{4}{8} = \frac{1}{2}$ and $x_2 = \frac{-16 - 20}{8} = \frac{-36}{8} = -\frac{9}{2}$.
Since the region must satisfy $y^2 \leq 4x$, we must have $x \ge 0$ (for real $y$). Thus, the only relevant intersection occurs at $x = \frac{1}{2}$.
Find the corresponding y-values using $y^2 = 4x$:
$y^2 = 4 \left(\frac{1}{2}\right) = 2$
$y = \pm \sqrt{2}$
The intersection points are $\left(\frac{1}{2}, \sqrt{2}\right)$ and $\left(\frac{1}{2}, -\sqrt{2}\right)$.
The region is bounded on the left by the parabola $x = \frac{y^2}{4}$ (from $y^2 = 4x$) and on the right by the circle $x = \sqrt{\frac{9}{4} - y^2}$ (from $x^2 + y^2 = \frac{9}{4}$, taking the positive root since the region is to the right of the parabola, implying $x \ge 0$ near the intersection).
The region extends vertically from $y = -\sqrt{2}$ to $y = \sqrt{2}$.
The area $A$ of the region can be found by integrating with respect to $y$:
$A = \int_{-\sqrt{2}}^{\sqrt{2}} \left(x_{\text{circle}} - x_{\text{parabola}}\right) dy$
$A = \int_{-\sqrt{2}}^{\sqrt{2}} \left(\sqrt{\frac{9}{4} - y^2} - \frac{y^2}{4}\right) dy$
Due to the symmetry of the region about the x-axis, we can integrate from $0$ to $\sqrt{2}$ and multiply the result by 2:
$A = 2 \int_{0}^{\sqrt{2}} \left(\sqrt{\frac{9}{4} - y^2} - \frac{y^2}{4}\right) dy$
$A = 2 \int_{0}^{\sqrt{2}} \sqrt{\left(\frac{3}{2}\right)^2 - y^2} \, dy - 2 \int_{0}^{\sqrt{2}} \frac{y^2}{4} \, dy$
$A = 2 \int_{0}^{\sqrt{2}} \sqrt{\left(\frac{3}{2}\right)^2 - y^2} \, dy - \frac{1}{2} \int_{0}^{\sqrt{2}} y^2 \, dy$
Evaluate the first integral using the formula $\int \sqrt{a^2 - y^2} \, dy = \frac{y}{2}\sqrt{a^2 - y^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{y}{a}\right)$, with $a = \frac{3}{2}$:
$2 \int_{0}^{\sqrt{2}} \sqrt{\left(\frac{3}{2}\right)^2 - y^2} \, dy = 2 \left[ \frac{y}{2}\sqrt{\frac{9}{4} - y^2} + \frac{9/4}{2}\sin^{-1}\left(\frac{y}{3/2}\right) \right]_{0}^{\sqrt{2}}$
$= 2 \left[ \frac{y}{2}\sqrt{\frac{9}{4} - y^2} + \frac{9}{8}\sin^{-1}\left(\frac{2y}{3}\right) \right]_{0}^{\sqrt{2}}$
Evaluating at the limits:
$= 2 \left( \left(\frac{\sqrt{2}}{2}\sqrt{\frac{9}{4} - (\sqrt{2})^2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)\right) - \left(\frac{0}{2}\sqrt{\frac{9}{4} - 0^2} + \frac{9}{8}\sin^{-1}\left(\frac{0}{3}\right)\right) \right)$
$= 2 \left( \frac{\sqrt{2}}{2}\sqrt{\frac{9}{4} - 2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) - 0 \right)$
$= 2 \left( \frac{\sqrt{2}}{2}\sqrt{\frac{1}{4}} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) \right)$
$= 2 \left( \frac{\sqrt{2}}{2} \cdot \frac{1}{2} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) \right)$
$= 2 \left( \frac{\sqrt{2}}{4} + \frac{9}{8}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right) \right) = \frac{\sqrt{2}}{2} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
Evaluate the second integral:
$-\frac{1}{2} \int_{0}^{\sqrt{2}} y^2 \, dy = -\frac{1}{2} \left[ \frac{y^3}{3} \right]_{0}^{\sqrt{2}}$
$= -\frac{1}{2} \left( \frac{(\sqrt{2})^3}{3} - \frac{0^3}{3} \right)$
$= -\frac{1}{2} \left( \frac{2\sqrt{2}}{3} \right) = -\frac{\sqrt{2}}{3}$
Add the results of the two integrals to find the total area:
$A = \left(\frac{\sqrt{2}}{2} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)\right) + \left(-\frac{\sqrt{2}}{3}\right)$
$A = \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{3} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
$A = \frac{3\sqrt{2} - 2\sqrt{2}}{6} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
$A = \frac{\sqrt{2}}{6} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)$
The area of the region is $\left(\frac{\sqrt{2}}{6} + \frac{9}{4}\sin^{-1}\left(\frac{2\sqrt{2}}{3}\right)\right)$ square units.
Choose the correct answer in the following Exercises from 16 to 20.
Question 16. Area bounded by the curve y = x3, the x-axis and the ordinates x = – 2 and x = 1 is
(A) -9
(B) $\frac{−15}{4}$
(C) $\frac{15}{4}$
(D) $\frac{17}{4}$
Answer:
Given:
Equation of the curve: $y = x^3$
Equation of the x-axis: $y = 0$
Ordinates (vertical lines): $x = -2$ and $x = 1$
To Find:
The area bounded by the curve, the x-axis, and the given ordinates.
Solution:
The area bounded by the curve $y = f(x)$, the x-axis, and the lines $x=a$ and $x=b$ is given by $\int_{a}^{b} |f(x)| \, dx$.
In this case, $f(x) = x^3$, $a = -2$, and $b = 1$.
The function $y = x^3$ is negative for $x < 0$ and positive for $x > 0$. Therefore, we need to split the integral into two parts: from $x = -2$ to $x = 0$ and from $x = 0$ to $x = 1$.
For $-2 \le x < 0$, $x^3 \le 0$, so $|x^3| = -x^3$.
For $0 \le x \le 1$, $x^3 \ge 0$, so $|x^3| = x^3$.
The total area $A$ is given by:
$A = \int_{-2}^{1} |x^3| \, dx = \int_{-2}^{0} |x^3| \, dx + \int_{0}^{1} |x^3| \, dx$
$A = \int_{-2}^{0} (-x^3) \, dx + \int_{0}^{1} x^3 \, dx$
Evaluate the first integral:
$\int_{-2}^{0} (-x^3) \, dx = \left[ -\frac{x^4}{4} \right]_{-2}^{0}$}
$= \left(-\frac{0^4}{4}\right) - \left(-\frac{(-2)^4}{4}\right)$
$= 0 - \left(-\frac{16}{4}\right) = 0 - (-4) = 4$
Evaluate the second integral:
$\int_{0}^{1} x^3 \, dx = \left[ \frac{x^4}{4} \right]_{0}^{1}$}
$= \frac{1^4}{4} - \frac{0^4}{4} = \frac{1}{4} - 0 = \frac{1}{4}$
Add the results of the two integrals to find the total area:
$A = 4 + \frac{1}{4} = \frac{16}{4} + \frac{1}{4} = \frac{17}{4}$
The area bounded by the curve y = x3, the x-axis and the ordinates x = – 2 and x = 1 is $\frac{17}{4}$.
Comparing this with the given options, we find that option (D) is correct.
The correct answer is (D) $\frac{17}{4}$.
Question 17. The area bounded by the curve y = x | x | , x-axis and the ordinates x = – 1 and x = 1 is given by
(A) 0
(B) $\frac{1}{3}$
(C) $\frac{2}{3}$
(D) $\frac{4}{3}$
[Hint : y = x2 if x > 0 and y = – x2 if x < 0].
Answer:
Given:
Equation of the curve: $y = x | x |$
Equation of the x-axis: $y = 0$
Ordinates (vertical lines): $x = -1$ and $x = 1$
To Find:
The area bounded by the curve, the x-axis, and the given ordinates.
Solution:
The curve $y = x|x|$ can be defined piecewise based on the value of $x$:
If $x \ge 0$, then $|x| = x$, so $y = x \cdot x = x^2$.
If $x < 0$, then $|x| = -x$, so $y = x \cdot (-x) = -x^2$.
Thus, the curve is $y = -x^2$ for $x < 0$ and $y = x^2$ for $x \ge 0$.
The area bounded by the curve $y = f(x)$, the x-axis, and the ordinates $x=a$ and $x=b$ is given by $\int_{a}^{b} |f(x)| \, dx$.
Here, $f(x) = x|x|$, $a = -1$, and $b = 1$. Since the definition of the function changes at $x=0$, and the function $y = x|x|$ is negative for $x<0$ and positive for $x>0$ (except at $x=0$), we need to split the integral at $x=0$.
For $-1 \le x < 0$, $y = -x^2$. Since $-x^2 \le 0$ in this interval, the curve is below the x-axis. The contribution to the area is $\int_{-1}^{0} |-x^2| \, dx = \int_{-1}^{0} x^2 \, dx$.
For $0 \le x \le 1$, $y = x^2$. Since $x^2 \ge 0$ in this interval, the curve is above the x-axis. The contribution to the area is $\int_{0}^{1} |x^2| \, dx = \int_{0}^{1} x^2 \, dx$.
The total area $A$ is the sum of these two areas:
$A = \int_{-1}^{0} x^2 \, dx + \int_{0}^{1} x^2 \, dx$
Evaluate the first integral:
$\int_{-1}^{0} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{-1}^{0}$
$= \left(\frac{0^3}{3}\right) - \left(\frac{(-1)^3}{3}\right)$
$= 0 - \left(-\frac{1}{3}\right) = \frac{1}{3}$
Evaluate the second integral:
$\int_{0}^{1} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{0}^{1}$}
$= \left(\frac{1^3}{3}\right) - \left(\frac{0^3}{3}\right)$
$= \frac{1}{3} - 0 = \frac{1}{3}$
The total area is the sum of the results:
$A = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}$
The area bounded by the curve y = x | x | , x-axis and the ordinates x = – 1 and x = 1 is $\frac{2}{3}$.
Comparing this with the given options, we find that option (C) is correct.
The correct answer is (C) $\frac{2}{3}$.
Question 18. The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
(A) $\frac{4}{3} (4π - \sqrt{3})$
(B) $\frac{4}{3} (4π + \sqrt{3})$
(C) $\frac{4}{3} (8π - \sqrt{3})$
(D) $\frac{4}{3} (8π + \sqrt{3})$
Answer:
Given:
The equation of a circle: $x^2 + y^2 = 16$.
The equation of a parabola: $y^2 = 6x$.
To Find:
The area of the circle that is exterior to the parabola.
Solution:
The equation of the circle is $x^2 + y^2 = 16$. This is a circle centered at the origin $(0,0)$ with radius $r = \sqrt{16} = 4$.
The equation of the parabola is $y^2 = 6x$. This is a parabola opening to the right with its vertex at the origin $(0,0)$.
To find the area of the circle exterior to the parabola, we first need to find the area of the region common to both the circle and the parabola. Then we subtract this common area from the total area of the circle.
First, let's find the points of intersection of the circle and the parabola by substituting $y^2 = 6x$ into the circle equation:
$x^2 + 6x = 16$
$x^2 + 6x - 16 = 0$
Factoring the quadratic equation:
$(x+8)(x-2) = 0$
This gives two possible x-values for intersection: $x = -8$ or $x = 2$.
Since the parabola $y^2 = 6x$ is defined only for $x \ge 0$ (as $y^2 \ge 0$), the intersection point $x = -8$ is not valid for the parabola. Thus, the only valid intersection occurs at $x = 2$.
Substitute $x=2$ into the parabola equation $y^2 = 6x$ to find the corresponding y-values:
$y^2 = 6(2) = 12$
$y = \pm\sqrt{12} = \pm 2\sqrt{3}$
The points of intersection are $(2, 2\sqrt{3})$ and $(2, -2\sqrt{3})$. These points lie on both the parabola and the circle.
The area common to the circle and the parabola is bounded by the parabola $y^2 = 6x$ from $x=0$ to $x=2$, and by the circle $x^2 + y^2 = 16$ from $x=2$ to $x=4$. This region is symmetric about the x-axis. We can calculate the area of the upper half ($y \ge 0$) and double it.
The upper half of the region common to both is bounded by $y = \sqrt{6x}$ from $x=0$ to $x=2$, and by $y = \sqrt{16 - x^2}$ from $x=2$ to $x=4$.
The area of the upper half ($A_{upper}$) is the sum of two integrals:
$A_{upper} = \int_0^2 \sqrt{6x} dx + \int_2^4 \sqrt{16 - x^2} dx$
Evaluate the first integral:
$\int_0^2 \sqrt{6x} dx = \sqrt{6} \int_0^2 x^{1/2} dx = \sqrt{6} \left[ \frac{x^{3/2}}{3/2} \right]_0^2 = \sqrt{6} \left[ \frac{2}{3} x^{3/2} \right]_0^2$
$= \sqrt{6} \left( \frac{2}{3} (2)^{3/2} - \frac{2}{3} (0)^{3/2} \right) = \sqrt{6} \frac{2}{3} (2\sqrt{2}) = \frac{4\sqrt{12}}{3} = \frac{4 \cdot 2\sqrt{3}}{3} = \frac{8\sqrt{3}}{3}$
Evaluate the second integral using the formula $\int \sqrt{a^2 - x^2} dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\arcsin\left(\frac{x}{a}\right)$, with $a=4$:
$\int_2^4 \sqrt{16 - x^2} dx = \left[ \frac{x}{2}\sqrt{16 - x^2} + \frac{16}{2}\arcsin\left(\frac{x}{4}\right) \right]_2^4$
$= \left( \frac{4}{2}\sqrt{16 - 4^2} + 8\arcsin\left(\frac{4}{4}\right) \right) - \left( \frac{2}{2}\sqrt{16 - 2^2} + 8\arcsin\left(\frac{2}{4}\right) \right)$
$= \left( 2\sqrt{0} + 8\arcsin(1) \right) - \left( 1\sqrt{12} + 8\arcsin\left(\frac{1}{2}\right) \right)$
$= \left( 0 + 8 \cdot \frac{\pi}{2} \right) - \left( 2\sqrt{3} + 8 \cdot \frac{\pi}{6} \right)$
$= 4\pi - \left( 2\sqrt{3} + \frac{4\pi}{3} \right) = 4\pi - 2\sqrt{3} - \frac{4\pi}{3} = \frac{12\pi - 4\pi}{3} - 2\sqrt{3} = \frac{8\pi}{3} - 2\sqrt{3}$
The area of the upper half common to both is:
$A_{upper} = \frac{8\sqrt{3}}{3} + \frac{8\pi}{3} - 2\sqrt{3} = \frac{8\pi}{3} + \frac{8\sqrt{3} - 6\sqrt{3}}{3} = \frac{8\pi}{3} + \frac{2\sqrt{3}}{3}$
The total area common to the circle and the parabola ($A_{common}$) is twice the upper half area due to symmetry:
$A_{common} = 2 \times A_{upper} = 2 \left( \frac{8\pi}{3} + \frac{2\sqrt{3}}{3} \right) = \frac{16\pi}{3} + \frac{4\sqrt{3}}{3}$
The total area of the circle is $A_{circle} = \pi r^2 = \pi (4^2) = 16\pi$.
The area of the circle exterior to the parabola is the total area of the circle minus the area common to both:
$A_{exterior} = A_{circle} - A_{common}$
$A_{exterior} = 16\pi - \left( \frac{16\pi}{3} + \frac{4\sqrt{3}}{3} \right) = 16\pi - \frac{16\pi}{3} - \frac{4\sqrt{3}}{3}$
$A_{exterior} = \frac{48\pi - 16\pi}{3} - \frac{4\sqrt{3}}{3} = \frac{32\pi}{3} - \frac{4\sqrt{3}}{3}$
We can factor out $\frac{4}{3}$ from this expression:
$A_{exterior} = \frac{4}{3} (8\pi - \sqrt{3})$
The area of the circle exterior to the parabola is $\frac{4}{3} (8\pi - \sqrt{3})$ square units.
Comparing this with the given options, we find that option (C) is correct.
The correct answer is (C) $\frac{4}{3} (8π - \sqrt{3})$.
Question 19. The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ $\frac{π}{2}$ is
(A) $2(\sqrt{2 − 1})$
(B) $\sqrt{2} - 1$
(C) $\sqrt{2} + 1$
(D) $\sqrt{2}$
Answer:
Given:
The bounding curves and lines are the y-axis ($x=0$), $y = \cos x$, $y = \sin x$, within the interval $0 \le x \le \frac{\pi}{2}$.
To Find:
The area bounded by the given curves and the y-axis in the specified interval.
Solution:
The area is bounded by the curves $y = \sin x$ and $y = \cos x$ from $x=0$ (the y-axis) to $x=\frac{\pi}{2}$.
First, we need to find the point(s) of intersection of the two curves $y = \sin x$ and $y = \cos x$ within the interval $0 \le x \le \frac{\pi}{2}$.
Set $\sin x = \cos x$.
Dividing by $\cos x$ (assuming $\cos x \ne 0$):
$\frac{\sin x}{\cos x} = 1$
$\tan x = 1$
In the interval $0 \le x \le \frac{\pi}{2}$, the value of $x$ for which $\tan x = 1$ is $x = \frac{\pi}{4}$.
So, the curves intersect at $x = \frac{\pi}{4}$.
We need to determine which function is greater in the intervals $[0, \frac{\pi}{4}]$ and $[\frac{\pi}{4}, \frac{\pi}{2}]$.
For $0 \le x < \frac{\pi}{4}$, $\cos x > \sin x$.
For $\frac{\pi}{4} < x \le \frac{\pi}{2}$, $\sin x > \cos x$.
The area between the curves is the sum of the areas in these two sub-intervals.
Area A = $\int_0^{\pi/4} (\cos x - \sin x) dx + \int_{\pi/4}^{\pi/2} (\sin x - \cos x) dx$
Evaluate the first integral:
$\int_0^{\pi/4} (\cos x - \sin x) dx = [\sin x - (-\cos x)]_0^{\pi/4} = [\sin x + \cos x]_0^{\pi/4}$
$= \left( \sin \frac{\pi}{4} + \cos \frac{\pi}{4} \right) - (\sin 0 + \cos 0)$
$= \left( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \right) - (0 + 1)$
$= \frac{2}{\sqrt{2}} - 1 = \sqrt{2} - 1$
Evaluate the second integral:
$\int_{\pi/4}^{\pi/2} (\sin x - \cos x) dx = [-\cos x - \sin x]_{\pi/4}^{\pi/2}$
$= (-\cos \frac{\pi}{2} - \sin \frac{\pi}{2}) - (-\cos \frac{\pi}{4} - \sin \frac{\pi}{4})$
$= (-0 - 1) - \left( -\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}} \right)$
$= -1 - \left( -\frac{2}{\sqrt{2}} \right) = -1 - (-\sqrt{2}) = \sqrt{2} - 1$
The total area A is the sum of these two areas:
A = $(\sqrt{2} - 1) + (\sqrt{2} - 1)$
A = $2\sqrt{2} - 2 = 2(\sqrt{2} - 1)$
The area bounded by the y-axis, $y=\cos x$, and $y=\sin x$ when $0 \le x \le \frac{\pi}{2}$ is $2(\sqrt{2} - 1)$ square units.
Comparing this with the given options, we find that option (A) is correct.
The correct answer is (A) $2(\sqrt{2 − 1})$.

